移相発振回路(トランジスタ)の実験

1. 実験の目的

バイポーラ・トランジスタを使用したCR移相発振回路の発振原理を
理解するととにも、回路を組み立て、発振動作を確認します。


2. 実験課題

下記の項目について測定を行い、設計値と測定値を比較します。

1. 発振波形の確認
2. 発振周波数
3. 発振電圧の振幅



3. 実験回路





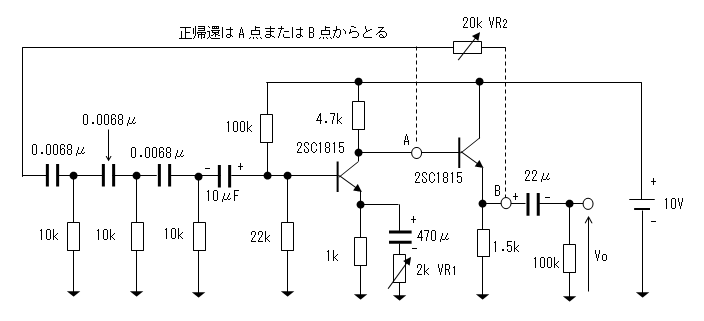
4. 回路構成と動作原理

反転増幅回路の出力をCRの微分回路3段により位相を180度回して(移相)から増幅回路の入力に
戻すことにより正帰還をかけると、増幅回路の入力にノイズなどにより発生した信号が
次第に増幅され、発振します。
このときの発振周波数は、移相回路でちょうど180度位相が回る周波数となります。
移相発振回路の詳細原理は電子回路− 移相発振回路の原理を参照してください。

増幅回路はトランジスタ2石により構成します。
初段はエミッタ接地増幅で、可変抵抗(2kΩ)により増幅度を29倍に設定します。
2段目のトランジスタはエミッタ・フォロワーで、出力インピーダンスを低くするとともに
負荷の変動により発振周波数が変動することを防ぎます。(緩衝増幅)


5. 回路定数の設計

1. 設計条件
(1)発振周波数: 約1[kHz]
(2)電源電圧: 10[V]
(3)出力電圧: 出たとこ勝負
(4)トランジスタ2石構成


2. トランジスタの直流バイアス設定
直流動作点となるバイアス設定については、トランジスタ増幅実験−2石直結増幅
(エミッタ接地〜コレクタ接地)で用いたものをそのまま流用しましたので
バイアス設計についてはそちらを 参照してください。


3. ゲイン調整
CR移相発振回路では、増幅回路の増幅度は-29倍必要となります。
ここで、マイナスは反転増幅であることを意味します。
増幅度を29倍に設定するために、初段のトランジスタの交流に対するエミッタ抵抗の値を
可変抵抗器にて調整することにより増幅度を加減します。
増幅回路の増幅度が29倍未満になると発振しません。
また、29倍より大きくし過ぎると、正弦波の波形の歪が大きくなります。
ただし、本回路ではもともと歪はあまり小さくはなりません。

初段のエミッタ接地の増幅回路では29倍以上の増幅度が必要ですが、コレクタとエミッタの抵抗は
直流バイアス設計によりすでに4.7[kΩ]と1[kΩ]に決めてしまいました。
そこで、交流的なエミッタ抵抗の値を変えるために、エミッタの1[kΩ]と並列に
470[μF]と2[kΩ]のVRを直列にした回路を接続し増幅度を調整します。
エミッタ接地増幅回路の増幅度は次の式で与えられます。
(いつものようにh_ieに概算式を代入しています。詳細はリンクを参照してください)
A_V1 = -R_C1/{1/(40 * I_C1) + R_E1}

この式から必要なR_Eを逆算します。
R_E1 = -R_C/Av - 1/(40 * I_C)
　= -4700 / (-29) - 1/(40 * 0.001)
∴ R_E ≒ 137[Ω]

この値を、1[kΩ]とVRで実現すればよいので、その時のVRの値は大体159[Ω]になるので
2[kΩ]VRで何とかなりそうです。(もう少し小さい方が調整が楽そうですが)


4. エミッタ・フォロワー
エミッタ・フォロワーの増幅度はほぼ1とみなしてよいでしょう。
また、初段のエミッタ接地の増幅度にも余裕があるので、エミッタ・フォロワーで多少の減衰が
あっても増幅回路全体としては必要な増幅度が確保できます。


5. 移相回路
CR移相発振回路の発振周波数fは
f = 1/(2π√6 CR)
で与えられます。
発振周波数を1kHzとしましたが、抵抗器の方が入手出来る定数の選択肢が広いので
まずコンデンサの値を選定し、それから必要な抵抗値がいくらになるか計算して
f=1kHzとなるコンデンサと抵抗器の組み合わせを決めます。

問題は増幅回路の入出力インピーダンスが有限であることです。
上記の周波数の計算式は、増幅器の出力インピーダンスが0で、入力インピーダンスが
無限大であること前提条件としています。
出力インピーダンスはエミッタ・フォロワーなので、数十Ωであり微分回路より
十分小さいインピーダンスと考えられます。
一方、トランジスタの入力インピーダンスが低いことは無視出来ません。

しかしまずは、増幅部のインピーダンスが無限大として計算してみます。
移相回路の抵抗の値を小さめにすると、コンデンサーの容量が大きくなってしまいます。
具体的に計算してみます。

仮に、抵抗を1[kΩ]とすれば、必要なコンデンサーの容量は
C = 1/(2π * √6 * f * R) = 1/(2π * √6 * 1000 * 1000) ≒ 0.065[μF]
抵抗を10[kΩ]とすれば、必要なコンデンサーの容量は
C = 1/(2π * √6 * f * R) = 1/(2π * √6 * 1000 * 10000) ≒ 0.0065[μF]

となります。
E6系列 のコンデンサーを使うとすれば、0.068[μF]か0.0068[μF]を使うことになるでしょう。

で、今回は、C=0.0068μF、R=10kΩとしました。
fを計算してみると、
f= 1/(2π√6×0.0068[μF]×10[kΩ])
≒956[Hz]

目標とする1kHzに対し、少し偏差が大きいようにも見えますが
もともとCR発振器は周波数の安定度もあまりよくないため、
正確な周波数の発振器の用途には向いていません。
もし、もっと正確な周波数で発振させたければ、別な回路構成とすべきなので
今回はこの定数で実験することにします。



6. 実験方法

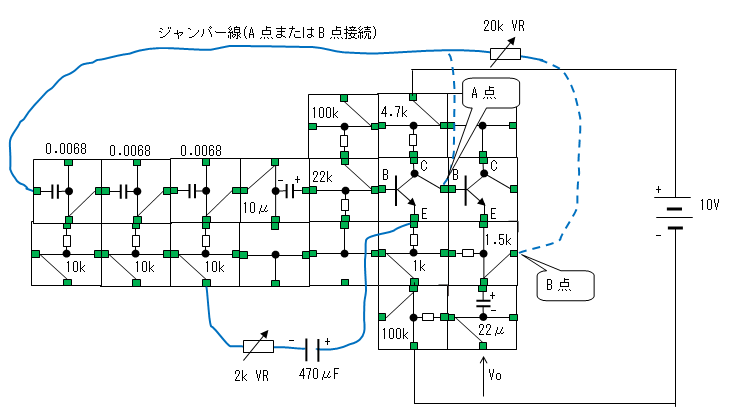
1. 電子ブロックの配置



2. 測定系全体接続



3. 発振波形の確認
Voの電圧波形をオシロスコープで観測します。


4. 発振周波数の確認
Voに周波数ブリッジおよび周波数測定レンジに設定したデジタル・テスターを
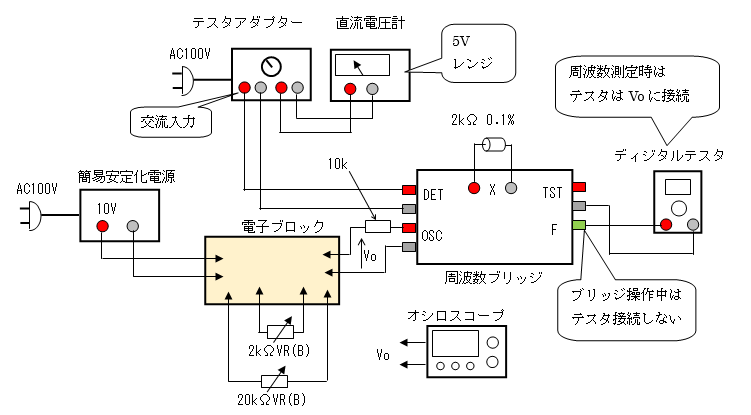
接続して測定しました。その際、Voと周波数ブリッジとの間に10[kΩ]の抵抗器を
接続しました。直接周波数ブリッジを接続すると、負荷が重たくなるせいか
Voの波形が歪んでしまいます。


5. 発振電圧の確認
Voの値をテスター・アダプタ＋直流電圧計で読んでも良かったのですが、
接続の変更が面倒だったので、オシロスコープでpeak to peakの値を
読み取りました。




7. 実験機材

1. 自作電子ブロック
使用したブロックは、実験方法の 電子ブロックの配置を参照。

2. 簡易安定化電源 (10[V]端子)
3. 可変抵抗器(2kΩB)
4. 可変抵抗器(20kΩB)
5. 固定抵抗器(10kΩ)
6. 電解コンデンサー(470μF)
7. テスターアダプタ
8. アナログ直流電圧計
9. オシロスコープ
10. 交流ブリッジ
11. 2kΩ 0.1% 固定抵抗器
12. ディジタル・テスター



8. 実験結果

1. 発振波形・発振電圧
• A点から帰還をかけた場合(波形)
まあまあの(?)の正弦波で、安定に発振しています。
2[kΩ]VRの設定値は概ね0〜30[Ω]で発振しましたが、0[Ω]のときは
波形の下限付近がややつぶれました。

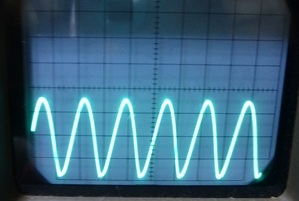
0.5mS/div、2V/div


• A点から帰還をかけた場合(周波数)
2[kΩ]VR(増幅度)の設定値により発振周波数は20〜30[Hz]ほど
変化しました。とりあえずの測定周波数は下記です。


周波数 ブリッジ測定		デジタル・ テスタ測定	設計値
1回目	31.2	947	956
2回目	32.5
3回目	33.2
平均[Ω] (これが抵抗Fの値)	32.3
周波数計算値 [Hz](*1)	1048
備考

(*1) 計算式：　f = 1/(2*π*C*F)、C=4.7[μF]


• B点から帰還をかけた場合(20kVR=0[Ω])
20kVR=0[Ω]とすると不思議なことに1k[Hz]では発振しません(-_-?
その代わり、よく見ると10[MHz]あたりで異常な発振をしています。
振幅は200[mV]p-pくらい。
この発振は、エミッタ・フォロワーのベースに47〜1[kΩ]の抵抗を
直列に入れても止まりませんでした。

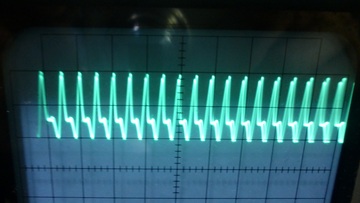
2μS/div、100mV/div


• B点から帰還をかけた場合(20kVR≒1.5[kΩ])
20kVRを増やしていくと低周波で間欠的に発振し始めます。
ただし、20kVRの設定値により波形は複雑に変化します。
下記の波形は一例です。

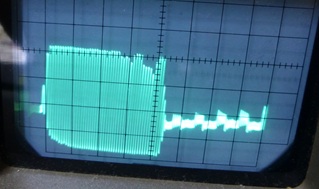
10mS/div、2V/div


• B点から帰還をかけた場合(20kVR≒4.2[kΩ])
20kVRの値を更に増やすと1[kHz]付近で連続で発振し始めましたが、
振幅が不安定です。振幅は7〜8[V]p-pほどです。

10mS/div、2V/div


• B点から帰還をかけた場合(20kVR≒4.2[kΩ])
前項と同じ条件で時間軸を引き延ばしました。
一応正弦波に見えます。

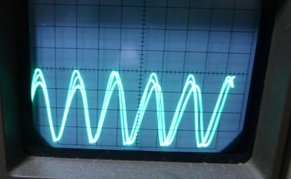
0.5mS/div、2V/div


• B点から帰還をかけた場合(周波数)
前項と同じ条件で周波数を測定しました。
2[kΩ]VR(増幅度)の設定値、および20[kΩ]VR(帰還量)の設定値により
発振周波数は20〜30[Hz]ほど変化します。
とりあえずの測定周波数は下記です。


周波数 ブリッジ測定		デジタル・ テスタ測定	設計値
1回目	33.8	1072 (*2)	956
2回目	39.6
3回目	25.1
平均[Ω] (これが抵抗Fの値)	32.8
周波数計算値 [Hz](*1)	1032
備考

(*1) 計算式：　f = 1/(2*π*C*F)、C=4.7[μF]
(*2) 必ずしも安定に測定出来ない。


• B点から帰還をかけた場合(20kVR≒9[kΩ])
さらに2kΩVRの値を増やすと、発振波形がまた異常になりました。
帰還量が減少したためと思われます。

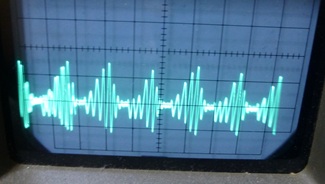
2mS/div、2V/div




9. 考察

1. A点から帰還をかけた場合
• 発振波形
オシロスコープで見ると、波形の下限付近がやや歪みが多いようですが、
もともと本回路は歪みの大きい回路なので、まずまずの正弦波だと思います。
発振は安定しています。


• 電圧振幅
およそ8[V]p-pの振幅となりましたが、電源電圧が10[V]であことから
増幅回路の最大振幅になると考えられます。


• 発振周波数
比較的設計値に近い周波数で発振しましたが、たまたまと思われます。
理想的な増幅回路に対し、実験回路の入力インピーダンスは低い一方、
逆に出力インピーダンスは高いことから、たまたま打ち消しあった結果と
推定します。周波数ブリッジでの測定はやや誤差が大きいようです。


2. B点から帰還をかけた場合
• 発振波形
2[kΩ]VR=0としたとき、1[kHz]で発振しないメカニズムが全く判りません。/(-_-)＼
また、2[kΩ]VRを調整し発振が始まっても、不安定で実用になるとは思えませんでした。
電子ブロックを使用したバラックの実験回路であることも影響した可能性も
ありますが、いずれにしてもA点から帰還をかけた方が安定です。


• 電圧振幅
およそ8[V]p-pの振幅となりましたが、電源電圧が10[V]であことから
増幅回路の最大振幅になると考えられます。


• 発振周波数
発振周波数は1[kHz]付近で、一応、計算値に近い値となりました。



10. 今後の課題

1. 2石構成発振回路
性能的には優れていると思われた2石構成でしたが、当初1[kHz]では全く発振せず、
1ヶ月以上悩んでしまいました。その後、帰還路にVR2を挿入すると発振することが
判明しましたが、何故そうなるのかは未だに不明です。
しかも、VR2を挿入しても、発振は不安です。
原因は不明のままですが、メカニズムの解析は今後の課題としました。


2. エミッタ・フォロワーの発振対策
前項と関連しますが、当初、1[kHz]で発振しない原因としてエミッタ・フォロワーの
異常発振を疑いました。一般的にエミッタ・フォロワーが発振し易いことの理論的考察と
対策は参考文献(2)に記述があり、重要な考察テーマですが、今回は検討を見送り、
後日改めて検討することにしました。



11. 参考文献

1. 定本続トランジスタ回路の設計(1992 初版) 14.2 CR発振回路の設計、鈴木雅臣著、CQ出版社
2. はじめてのトランジスタ回路設計(1999 初版) P-108〜112 2石で組むエミッタ・フォロワ、 黒田徹著、CQ出版社



12. 関連項目

1. 電子回路−移相発振回路の原理
2. トランジスタ増幅実験−2石直結増幅
3. 実験用安定化電源−簡易安定化電源 (10[V]端子)
4. 実験用小物ツール−可変抵抗器(2kΩB)
5. テスターアダプタ
6. アナログ直流電圧計
7. 交流ブリッジ
8. 実験用小物ツール−2kΩ 0.1% 固定抵抗器