移相発振回路の原理

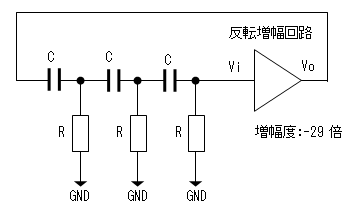
1. 原理図

基本的な回路構成は下図となります。
反転増幅回路の出力VoをCR回路3段による移相回路により180度位相を
ずらして増幅回路の入力に戻すと正帰還がかかり発振します。




2. 動作原理


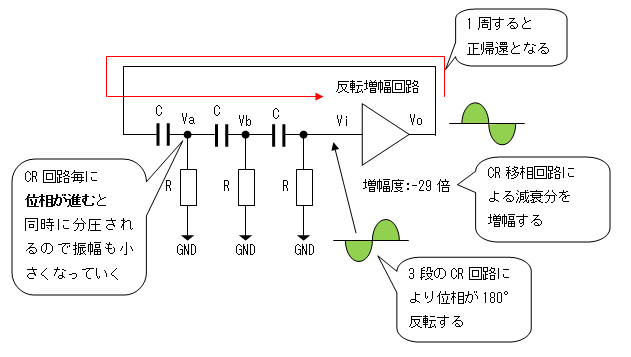
増幅度が-29倍の反転増幅回路とCRが3段(以上)の移相回路により構成されます。
反転増幅器により入力電圧Viと出力電圧Voとは位相が180度ずれています。
帰還回路により、出力電圧Voの位相を更に180度ずらして増幅器の入力に加えると
全体で360度位相がずれ元に戻るため、正帰還がかかり位相条件を満足するようになります。

位相を変えるためにCRによる微分回路を使用します。
(積分回路を使用する方式もある。)
1段のCR回路で90度未満の位相を変えられるので、180度位相を変えるためには
最低3段のCR回路が必要になります。


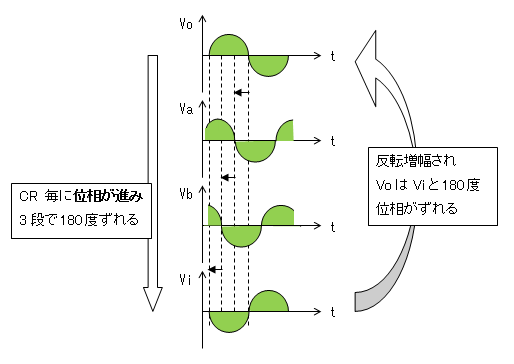
増幅度の29倍とゆうのは、3段のCR移相回路による損失が1/29であるためです。
この増幅度が29倍より小さいと、回路は発振しません。
正帰還された信号が、次第に減衰してしまうためです。
また、29倍よりあまり大きいと、正弦波の歪が大きくなります。
歪の小さな発振回路とするためには増幅回路にAGC(自動利得制御)などの
回路を付加する必要があります。
このような工夫をしない限り、一般的に、本回路が生成する正弦波の歪は大きいです。



3. 発振条件の計算

それぞれ3個あるCとRの値は必ずしも同じ値である必要はありませんが、
異なる値とすると発振周波数の計算が煩雑になること、
また使用する部品の種類が増えてしまうことから
通常は3個とも同じ値を使用します。

また、以下の計算では増幅回路の入力インピーダンスは無限大、
出力インピーダンスが零であることを前提としているため
実際の回路でこれらの条件からずれる場合は発振周波数が若干、
計算式からずれることになります。

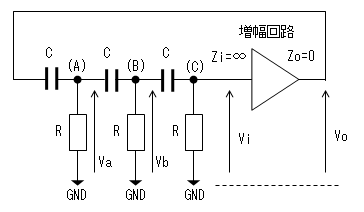
CR回路の電流I₁〜I₃を下図のように決めてキルヒホッフの電圧則を適用します。


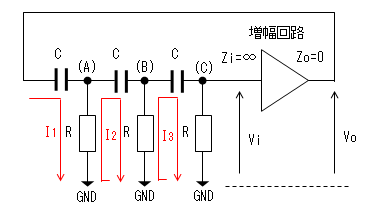
I₁〜I₃のループ毎に方程式を立てます。
1/(jωC) * I₁ + R * (I₁ - I₂) = V_o
R * (I₂ - I₁) + 1/(jωC) * I₂ + R * (I₂ - I₃) = 0
R * (I₃ - I₂) + 1/(jωC) * I₃ + R * I₃ = 0

それぞれの方程式について、I₁〜I₃の項ごとに纏めると
{1/(jωC) + R} * I₁ - R * I₂ = V_o
-R * I₁ + {2R + 1/(jωC)} * I₂ - R * I₃ = 0
-R * I₂ + {2R + 1/(jωC)} * I₃ = 0

この連立方程式を行列で表すと


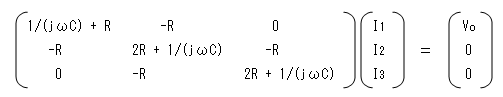
クラメルの公式(線形代数の教科書を参照してください。)を使って解きます。
まず行列式Δを次式で定義して、計算します。

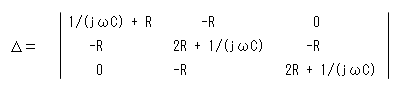
= {1/(jωC) + R} * {2R + 1/(jωC)}² - (-R)² * {1/(jωC) + R} - (-R)² * {2R + 1/(jωC)}
= {1/(jωC) + R} * {(2R)² + 4R/(jωC) + 1/(jωC)²} - R² * {1/(jωC) + R} - R² * {2R + 1/(jωC)}
= {1/(jωC) + R} * {4R² + 4R/(jωC) - 1/(ωC)²} - R²/(jωC) - R³ - 2R³ - R²/(jωC)
= 4R²/(jωC) + 4R/(jωC)² - 1/{j(ωC)³} + 4R³ + 4R²/(jωC) - R/(ωC)² - 3R³ - 2R²/(jωC)
= 6R²/(jωC) - 5R/(ωC)² - 1/{j(ωC)³} + R³
= 1/(jωC) * {6R² - 1/(ωC)²} - 5R/(ωC)² + R³

少したいへんでした。(-_-;
次に、行列式Δ₃を次式で定義して、計算します。
こちらは行列式の要素に0が多いので、たいへんではありません。(^^v

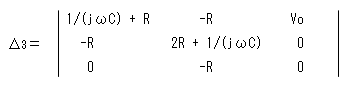
= (-R)² * Vo = R² * Vo

そうするとI₃は
I₃ = Δ₃ / Δ = R² * Vo / [1/(jωC) * {6R² - 1/(ωC)²} - 5R/(ωC)² + R³]

Viはi₃にRをかけたものです。そしてViをVoで割ったものが帰還率Fです。
Vi = i₃ * R
F = Vi / Vo = i₃ * R / Vo
　= R² * Vo / [1/(jωC) * {6R² - 1/(ωC)²} - 5R/(ωC)² + R³] * R / Vo
　= R³ / [1/(jωC) * {6R² - 1/(ωC)²} - 5R/(ωC)² + R³]

増幅器の増幅度をGとします。ただし、Gは実数とします。
バルクハウゼンの発振条件を 見つけるためにFGを計算すると
FG = R³ / [1/(jωC) * {6R² - 1/(ωC)²} - 5R/(ωC)² + R³] * G

周波数条件よりFGの虚数部が0になるためには、分母の虚数部である第1項が0になればよいので
6R² - 1/(ωC)² = 0
∴ 6R² = 1/(ωC)²
∴ ω² = 1 / (6R² * C²)　・・・・・・　(1)

周波数f = ω/(2π)ですので
f = 1 / (2π * √6 * CR)

FGの虚数部が0のとき、F(の実数部)*G=1が振幅条件なので
R³ / { - 5R/(ωC)² + R³} * G = 1
∴ G = { - 5R/(ωC)² + R³} / R³
∴ G = { - 5/(ωC)² + R²} / R²

この式に(1)式を代入してωを消去すると
G = ( - 5 * 6R² + R²) / R²
　= ( - 30R² + R²) / R²
　= - 29R² / R²
　= - 29
∴ G = -29

すなわち、増幅度29倍の反転増幅器が必要なことが判ります。



4. VaとVbの位相

実は、以前、3つのCR回路でそれぞれ60°づつ均等に位相がずれると
思っていたのですが、最近、間違っていることに気づきました。orz
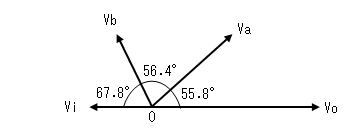
3つあるCR回路が相互に干渉するので、全体では180°ずれますが、それぞれの
CR回路での位相差は下図のように少しづつ違います。
(まあ、だいたい60°かもしれないけど。笑)



多少、細かい話ですので、違っていることを知っていれば十分で、
具体的な値はあまり重要ではないと思いますが、以下、計算結果です。
VaとVbは下図の(A)点、(B)点における電圧です。


まず、Δの虚数部を0とおいて、さらに(1)式を代入して簡単にしておきます。これをΔ'とします。
Δ' = -5R/(ωC)² + R³
　= -5R * (6R² * C²) / C² + R³
∴ Δ' = -29R³

次に、I₁とI₂を計算します。
そのために行列式Δ₁とΔ₂を以下の式で定義して、計算します。

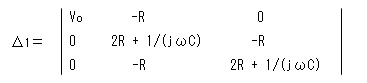
= Vo * {2R + 1/(jωC)}² - (-R)² * Vo = [{2R + 1/(jωC)}² - R²] * Vo


= -Vo * (-R) * {2R + 1/(jωC)} = {2R² + R/(jωC)} * Vo

それぞれの式に(1)式を代入してωを消去します。
Δ₁ = {(2R - j√6R)² - R²} * Vo
　= {(2 - j√6)² * R² - R²} * Vo
　= {(4 - j4√6 - 6) - 1} * R² * Vo
　= (-3 - j4√6) * R² * Vo

Δ₂ = {2R² + R/(jωC)} * Vo
　= {2R² - j√6R²} * Vo
　= (2 - j√6) * R² * Vo

そうすると
I₁ = Δ₁ / Δ' = (-3 - j4√6) * R² * Vo / (-29R³) = (3 + j4√6) * Vo / 29R
I₂ = Δ₂ / Δ' = (2 - j√6) * R² * Vo / (-29R³) = (-2 + j√6) * Vo / 29R

I₃の式についても、虚数部=0とおいてから、(1)式を代入してωを消去します。
I₃ = R² * Vo / { - 5R/(ωC)² + R³}
　= R² * Vo / ( - 5R * 6R² + R³)
　= R² * Vo / ( - 30R³ + R³)
　= R² * Vo / ( - 29R³)
　= -Vo / 29R

I₁〜I₃が求まったので、V_AとV_Bを計算します。
V_A = (I₁ - I₂) * R
　= {(3 + j4√6) * Vo / 29R - (-2 + j√6) * Vo / 29R} * R
　= {(3 + j4√6) - (-2 + j√6)} * (Vo / 29R) * R
　= (5 + j3√6) * Vo / 29

V_B = (I₂ - I₃) * R
　= {(-2 + j√6) * Vo / 29R - (-Vo / 29R)} * R
　= {(-2 + j√6) + 1} * (Vo / 29R) * R
　= (-1 + j√6) * Vo / 29

Voに対するVaとVbの位相をそれぞれθa、θbとすれば
θa = tan^-1 (3√6 / 5) ≒ 55.8°
θb = tan^-1 {√6 / (-1)} + 180 ≒ -67.8 + 180 = 112.2°

VaとVbの位相差は
θb - θa = 112.2° - 55.8° = 56.4°

VbとViの位相差は
180 - θb = 180° - 112.2° = 67.8°

となりますので、ベクトル図で書くと下記の結果(再掲)となります。




5. VaとVbの位相(別計算)

重要ではない、と書いておいて、くどいのですが別な計算方法です。(^o^;
計算結果が正しいことを確認するために試みました。
当然、結果は同じになります。


VbとViとの位相差は、Vbに対してViがいくらになるかを計算すると求まります。すなわち
Vi = R / {1/(jωC) + R} * Vb

(1)式を代入してωを消去すると
Vi = R / (-j√6R + R) * Vb
　= 1 / (1 - j√6) * Vb
　= (1 + j√6) / {(1 - j√6) * (1 + j√6)} * Vb
　= (1 + j√6) / (1 + √6) * Vb

よって、VbとViとの位相差は
tan^-1(√6/1) ≒ 67.8°

VaとVbとの位相差は、Vaに対してVbがいくらになるかを計算すると求まります。少し複雑です。
Vb = [R // {1/(jωC) + R}] / [1/(jωC) + R // {1/(jωC) + R}] * Va

(1)式を代入してωを消去すると
Vb = {R // (-j√6R + R)} / {-j√6R + R // (-j√6R + R)} * Va
　 = {R * (-j√6R + R) / (R - j√6R + R)} / {-j√6R + R * (-j√6R + R) / (R - j√6R + R)} * Va
　 = {R * (-j√6R + R) / (2R - j√6R)} / {-j√6R + R * (-j√6R + R) / (2R - j√6R)} * Va
　 = {(-j√6R + R) / (2 - j√6)} / {-j√6R + (-j√6R + R) / (2 - j√6)} * Va

分母・分子に(2 - j√6)をかけます
Vb = (-j√6R + R) / {-j√6R * (2 - j√6) + (-j√6R + R)} * Va
　 = (-j√6R + R) / {-j2√6R - 6R + (-j√6R + R)} * Va
　 = (-j√6R + R) / (-j3√6R - 5R) * Va
　 = (-j√6 + 1) / (-j3√6 - 5) * Va
　 = (-1 + j√6) / (5 + j3√6) * Va

分母を実数化します。
Vb = {(-1 + j√6) * (5 - j3√6)} / {(5 + j3√6)* (5 - j3√6)} * Va
　 = {-5 + j3√6 + j5√6 + 18} / (25 + 54) * Va
　 = (13 + j8√6) / 79 * Va

よって、VaとVbとの位相差は
tan^-1(8√6/13) ≒ 56.4°

VoとVaとの位相差は、
180 - (67.8 + 56.4) = 55.8°

前項と同じ結果となりました。




6. 関連項目

1. 電気回路−交流理論
2. キルヒホッフの法則
3. クラメルの方法



7. 参考文献

1. アナログ電子回路の基礎(2003 第1版第1刷) 第11章 発振回路、堀桂太郎著、東京電機大学出版局
2. 電子回路の基礎マスター(2009 第1版第1刷) 第4章 発振回路、堀桂太郎監修・船倉一郎著、電気書院
3. 電子回路(平成20(2008)年 第1版第1刷) 9章 発振回路、岩田聡編著、オーム社
4. 電子回路A(平成8(1996)年 第1版第2刷) 第8章 発振回路の働き、藤原修編著、オーム社
5. 定本続トランジスタ回路の設計(1992 初版) 14.2 CR発振回路の設計、鈴木雅臣著、CQ出版社