エミッタ接地増幅回路(交流負帰還あり)の実験 デジタルテスターによる

1. 実験の目的

   電流帰還バイアスをかけたトランジスタ増幅器において、エミッタ抵抗(R_E)に
   並列に接続するバイパス・コンデンサを無くすと、交流的に負帰還をかける
   ことが出来ます。ここでは、負帰還の量を変化させることにより、
   増幅回路の入力インピーダンス、出力インピーダンス、増幅度が
   どのように変化するか理論と実験で確認します。
   
   

2. 実験課題

   下記の項目について測定を行い、設計値と測定値を比較します。
   増幅度については、負帰還の量を変化させ、増幅度との関係を調べます。
   
   
   1. 増幅度
   2. 入力インピーダンス
   3. 出力インピーダンス
   
   

3. 実験回路

   実験回路を下図に示します。
   出力側に接続した抵抗器:R_Lは、出力電圧の直流レベルを確定するために
   接続しました。この抵抗がないと、電源投入時、出力コンデンサ:Coの電荷が0で
   あるため、Coの両端の電圧が0となり、出力波形の直流レベルが浮き上がります。
   交流信号に対してR_L接続の影響が出ないように、R_L >> Rcとなる
   値を選定しました。
   また、回路設計の中で出てくるR_E(AC)は抵抗R_Eのタップの中の
   バイパス・コンデンサC_Eを接続した点とトランジスタのエミッタ端子間の抵抗値を
   示します。(すなわち、交流に対するR_Eの値です)
   
   
   

4. 回路の動作

   電流帰還バイアスをかけたトランジスタ増幅器において、エミッタ抵抗R_Eに
   並列に接続するバイパス・コンデンサを無くすと、エミッタ電流icの変化により
   エミッタ抵抗(R_E)の両端に、
   ve = ie * R_E = (hfe+1) * ib * R_E
   
   となる交流電圧veが発生します。
   もし、エミッタ抵抗R_Eと並列にハイパス・コンデンサが接続させていればve=0となり、
   負帰還はかかりません。
   ベース〜エミッタ間の電圧は直流的に約0.7Vの差であるため
   エミッタに交流電圧veが発生すると、この交流電圧の変化は同時に
   ベース電圧の変化をもたらし、その方向はベース電流の変化を妨げる
   方向であるため、結果、負帰還として動作します。
   
   
   

5. 実験回路の設計

   1. 設計条件
      
      (1)電源は乾電池1.5V×4本=6Vとします。
      (2)コレクター電流:Ic=1mA
      (3)エミッタ抵抗R_Eの両端の電圧:V_E=1V
      (4)コレクタ抵抗Rcの両端の電圧:Vc=2.5V
      (5)トランジスタは2SC1815のYランクを使う(データシートよりh_FE=120〜240)
      (6)増幅する周波数帯域の最低周波数は50Hz
      (7)入力側(信号源)の出力インピーダンスは0[Ω] (実験では10[Ω])
      (8)出力側(負荷)の入力インピーダンスは∞。(Co計算時は1kと仮定)
      
      
      
   2. バイアス回路の設計
      バイアス回路の設計手順については、 負帰還のないエミッタ接地増幅回路と
      同じであるため、ここでは省略しますが、R_Eの値が1.1kΩ(= 220×5本)となり
      わずかに異なるため、改めて各部の電圧・電流を計算すると、
      結果は下記となります。
      　V1 = R2/(R1 + R2) * Vcc = 22[kΩ]/(47[kΩ] + 22[kΩ]) * 6[V] ≒ 1.9[V]
      　V_E = V2 - V_BE = 1.9[V] - 0.7[V] = 1.2[V]
      　I_E = V_BE/R_E = 1.2[V]/1.1[kΩ] = 1.1[mA]
      　Ic ≒ I_E = 1.1[mA]
      　Vc = Rc * Ic = 2.2[kΩ] * 1.1[mA] ≒ 2.4[V]
      　V_CE = Vcc - Vc - V_E = 6 - 2.4 - 1.2 = 2.4[V]
      
      
      
      
   3. 増幅回路の等価回路
      
      交流の等価回路ではカップリング・コンデンサのCi、Coは
      短絡して考えます。増幅する周波数帯ではコンデンサのリアクタンスが十分小さく
      なるように値を決めるため、交流的には短絡して考えるのですが、
      その値を決めるためには、入力インピーダンスの計算が必要なので、
      手順が前後するように見えますが、まず、増幅回路の等価回路から
      2個のコンデンサCi、Coを短絡した下図の等価回路で考えます。
      トランジスタはエミッタ接地の 小信号簡略等価回路に置き換え、
      また、Vccとグランド(GND)も交流的には同電位なので接続してあります。
      
      
      計算にあたってhieの値が必要になりますが、 概算式である
      hie = β/(40 * Ic)
      
      の式を用います。
      バイアス回路の設計の項で記述したように、今回の実験回路では、Ic =1.1[mA]です。
      また、本実験に使用するトランジスタのβは 静特性の測定実験で測定した値を
      使用すると175になりますので
      hie = β/(40 * Ic) = 175/(40 * 0.0011)
      ∴hie=3977[Ω]
      
      となります。
      
      
      
   4. 入力インピーダンスの計算
      まず、トランジスタのベースから右側を見たときの入力インピーダンスRiを
      計算します。Riの値は等価回路から
      Ri = vi/ib = hie + R_E * (hfe + 1)
      　= 3977 + 1100 * (175 + 1)
      　≒ 197.6[kΩ]
      
      ちなみに、
      hie << R_E * (hfe + 1)
      としてRi = R_E * hfeの式で概算すると
      Ri = 1100 * 175 = 192.5[kΩ]
      なので実用上、十分な近似となります。
      
      このRiを使用すると、Ziは
      Zi = R1//R2//Ri
      　= 47k // 22k // 197.6k
      ∴Zi = 13.9[kΩ]
      
      となります。
      本実験においては小信号(AC)に対するRi(AC)を220、440、660、880、1100
      と変化させることにより、負帰還量を変えながら測定します。
      以下、R_E(AC)を変えた場合についてZiを計算すると、
      

      RE(AC)	220	440	660	880	1100
      精密な計算式	11.1k	12.7k	13.3k	13.7k	13.9k
      概算式	10.8k	12.6k	13.3k	13.7k	13.9k

      
      
   5. 出力インピーダンスの計算
      制御電流源のインピーダンスは無限大であるため、等価回路より、
      Zo = Rc = 2200[Ω]
      となります。
      
      
      
   6. 増幅度の計算
      R_E(AC)=1100[Ω]の場合について計算します。
      精密な計算式を用いて計算すると
      Av = - Rc/{1/(40 * Ic) + R_E}
      　= - 2200/{1/(40 * 0.0011) + 1100}
      ∴Av = - 1.96
      
      概略の式を用いて計算すると
      Av = - Rc/R_E
      　= - 2200/1100
      ∴Av = - 2
      
      以下、R_E(AC)を変えた場合についてAvを計算すると、
      

      RE(AC)	220	440	660	880	1100
      精密な計算式	-9.06	-4.75	-3.22	-2.44	-1.96
      概算式	-10	-5	-3.3	-2.5	-2

      
      
   7. コンデンサの容量の決定
      (1)実験回路の等価回路
      トランジスタをエミッタ接地の 小信号簡略等価回路に置き換え、
      また、VccとGNDは交流的には同電位であることから接続してしまうと
      実験回路の小信号等価回路は下図のようになります。
      
      
      (2)入力コンデンサ(Ci)
      入力コンデンサCiの影響がないように定数を決定します。
      R1、R2、Riの並列回路の合成抵抗をZiとします。すなわち
      Zi = R1//R2//Ri
      
      とすれば、ZiとCiはローカット・フィルター(Low Cut Filer)を構成するため
      Ciの値が小さいと増幅する周波数帯域の低域側で増幅度が
      低下してしまいます。この影響をなくすためには、
      フィルタのカットオフ周波数が信号の最低周波数より
      十分小さくなるようにCiを決定します。
      
      
      このローカット・フィルターのカットオフ周波数fciは、
      fci = 1/(2π * Ci * Zi)
      となりますので、信号の最低周波数をfslとすれば
      fsl >> fci
      
      となるようにCiを決定すればよいことになります。よって
      fsl >> 1/(2π * Ci * Zi)
      ∴Ci >> 1/(2π * fsl * Zi)
      
      本実験においては、R_E(AC)を可変しながら測定しますが
      R_E(AC)=0のときに最もfciが高くなります。
      これは、負帰還がないのと同じ状態なので、Ri=hie=3977[Ω]として計算すると
      Zi = R1//R2//hie = 47k//22k//3.977k = 3144[Ω]
      
      入力信号の最低周波数(fsl)を50[Hz]でしたので、
      Ci >> 1/(2π * fsl * R) = 1/(2π * 50 * 3144) ≒ 1.01[μF]
      
      電解コンデンサは経年変化により静電容量が減少しますので、
      少なくとも計算値の2倍は欲しいところです。
      今回は、計算値より大き目の10[μF]とします。
      
      (3)出力コンデンサ(Co)　　　---(2024/09/28 修正)
      出力コンデンサCoの影響がないように定数を決定します。
      本増幅回路の次段の回路の入力抵抗:R_Lとすれば、
      RcとR_LとCoはローカット・フィルター(Low Cut Filer)を構成するため
      Coの値が小さいと増幅する周波数帯域の低域側で増幅度が
      低下してしまいます。この影響をなくすためには、
      フィルタのカットオフ周波数が信号の最低周波数より
      十分小さくなるようにCoを決定します。
      　
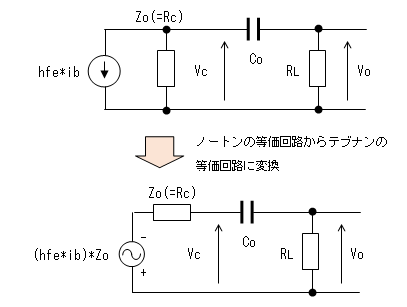
      (ノートンの等価回路からテブナンの等価回路への変換は こちら。)
      
      このローカット・フィルターのカットオフ周波数fcoは、
      fco = 1/(2π * Co * R_L)
      fco = 1/{2π * Co * (Rc + R_L)}
      となりますので、信号の最低周波数をfslとすれば
      fsl >> fco
      
      となるようにCoを決定すればよいことになります。よって
      fsl >> 1/(2π * Co * R_L)
      ∴Co >> 1/(2π * fsl * R_L)
      fsl >> 1/{2π * Co * (Rc + R_L)}
      ∴Co >> 1/{2π * fsl * (Rc + R_L)}
      
      入力信号の最低周波数(fsl)を50[Hz]とします。
      R_L=1[kΩ](実験の際のR_Lとは値が異なる)と仮定して、計算すると
      Co >> 1/(2π * fsl * R) = 1/(2π * 50 * 1000) ≒ 3.18[μF]
      Co >> 1/{2π * fsl * (Rc + R_L)} = 1/{2π * 50 * (2200 + 1000)} ≒ 0.99[μF]
      
      電解コンデンサは経年変化により静電容量が減少しますので、
      少なくとも計算値の2倍は欲しいところです。
      今回は、計算値より大き目の22[μF]とします。
      
      (4)バイパス・コンデンサ(C_E)
      負帰還なしのエミッタ接地増幅回路 で計算した値を使用します。
      従って、C_E = 470[μF]
      
      
      

6. 実験方法

   信号源としては、トランス・ボックス を使用します。
   従って、周波数は(東日本では)50Hzになります。
   トランス・ボックスの出力電圧がそのままでは電圧が高過ぎるので
   3.3kΩと10Ωの抵抗器により分圧し、20mV(rms)程度まで減衰させます。
   このとき、アッテネータとしてグランドとの間に10Ωを使用すると
   増幅器からみたときの信号源のインピーダンスが10Ωと低く
   抑えられるので、実験には好都合です。
   
   
   測定には5kΩの可変抵抗器、 20kΩの可変抵抗器、ディジタル・テスターの
   交流電圧測定機能を使用して、簡易測定法により、電圧増幅度、
   入力インピーダンス、出力インピーダンスをそれぞれ測定します。
   
   
   
   1. 電子ブロックの配置
      
      
      
   2. 電圧増幅度の測定
      増幅回路における電圧増幅度の簡易測定法によります。
      
      (1)下図の測定回路を組立てます。
      
      
      (2)R_E(AC)の値を設定します。
      (3)vsの値を読みます。
      (4)voの値を読みます。
      (5)vsの値に減衰回路の減衰比をかけてviを求めます。
      　今回の回路では、減衰比は10/3310になります。
      (6)viの値とvoの値から電圧増幅度Av=vo/viを求めます。
      (7)R_E(AC)の値を220、440、660、880、1100と変えながら
      　(2)〜(6)の測定を繰り返します。
      
      
   3. 入力インピーダンスの測定
      増幅回路における入力インピーダンスの簡易測定法によります。
      
      (1)下図の測定回路を組立てます。
      
      
      (2)R_E(AC)の値を設定します。
      (3)VRを0[Ω]の状態にしてvoの値を読み取ります。
      　この時のvoの読みをvo0とします。
      (4)voの値が1/2*vo0となるようにVRを調整します。
      (5)VRを回路から外し、テスターの抵抗レンジでVRの値を読み取ります。
      　この時のVRの値がZiとなります。
      (6)R_E(AC)の値を220、440、660、880、1100と変えながら
      　(2)〜(5)の測定を繰り返します。
      
      
   4. 出力インピーダンスの測定
      増幅回路における出力インピーダンスの簡易測定法によります。
      
      (1)下図の測定回路を組立てます。
      
      
      (2)R_E(AC)の値を設定します。
      (3)SWを開放の状態にしてvoの値を読み取ります。
      　この時のvoの読みをvo0とします。
      (4)SWを閉じて(短絡)からvoの値が1/2*vo0となるようにVRを調整します。
      (5)VRを回路から外し、テスターの抵抗レンジでVRの値を読み取ります。
      　この時のVRの値がZoとなります。
      (6)R_E(AC)の値を220、440、660、880、1100と変えながら
      　(2)〜(5)の測定を繰り返します。
      
      なお、SWについては、実際は配線を取り外すことにより解放しました。
      
   
   

7. 実験機材

   1. 電子ブロック
      
      使用したブロックは、実験方法の 電子ブロックの配置を参照。
      
   2. トランス・ボックス
   3. 5kΩの可変抵抗器
   4. 20kΩの可変抵抗器
   5. 固定抵抗器：3.3kΩ(1%)、10Ω(1%)
   6. ディジタル・テスター
   7. 乾電池：1.5V×4本、乾電池ホルダー
   8. 配線材
   
   

8. 実験結果

   1. 電圧増幅度の測定
      viの値は、vsの値に減衰比=10/3310をかけて算出しました。
      また、Av = - vo/vi　です(Av > 0としました)。
      

      vsの値　[V]	viの値　[mV]	RE [Ω]	voの値　[mV]	Av(測定値)	Av(精密計算値)	Av(概算計算値)	備考
      6.75	20.4	1100	37	1.8	1.96	2
      		880	48	2.4	2.44	2.5
      		660	64	3.1	3.22	3.3
      		440	95	4.7	4.75	5
      		220	185	9.1	9.06	10

      
      
      
      
   2. 入力インピーダンスの測定
      

      RE [Ω]	voの値　[mV]	vo/2の値　[mV]	Zi [kΩ] (測定値)	Zi [kΩ] (精密計算値)	Zi [kΩ] (概算計算値)	備考
      1100	38	19	11.7	13.9	13.9
      880	48	24	11.7	13.7	13.7
      660	64	32	11.8	13.3	13.3
      440	96	48	11.1	12.7	12.6
      220	185	92	10.1	11.1	10.8

      
      
      
      
   3. 出力インピーダンスの測定
      

      RE [Ω]	voの値　[mV]	vo/2の値　[mV]	Zi [kΩ] (測定値)	Zi [kΩ] (計算値)	備考
      1100	38	19	2.63	2.2
      880	48	24	2.69	2.2
      660	63	32	2.61	2.2
      440	96	48	2.36	2.2
      220	185	92	2.26	2.2

      
      
      
      

9. 測定結果・考察

   1. 電圧増幅度の測定
      測定値と精密計算値はよく一致しました。
      また、測定値と概算計算値は負帰還量が大きい程よく一致しました。
      実用上は、概算計算値で十分と考えられます。
      概算式Av = - Rc/R_Eは、抵抗器の値だけでAvを決定出来るため
      回路設計上、たいへん便利です。
      
      
   2. 入力インピーダンスの測定
      精密計算値と概算計算値とはほとんど差がないため、概算計算式 Zi=R1//R2で
      十分であると考えられます。
      測定値と計算値は10%〜20%の差があり、やや大きくなりました。
      
      
   3. 出力インピーダンスの測定
      測定値と計算値は最大20%近い差があり、やや大きくなりました。
      
   
   

10. 今後の課題

    1. 周波数特性の測定
       周波数特性は増幅回路の基本的な特性のひとつですが、今回の実験では
       信号源として発振器ではなく、トランス・ボックスを使用する方針としたので
       周波数特性の測定は断念しました。
       
       
    2. ひずみ率の測定
       用途によってはひずみ率も重要な特性ですが、ひずみ率計が手元にないため
       将来の課題としました。
       
    
    

11. 参考文献

    1. 定本トランジスタ回路の設計(1991 初版)、鈴木雅臣著、CQ出版社
       
    2. トランジスタ技術SPECIAL No.60 実験で学ぼう回路技術のテクニック(1997)、CQ出版社
       　実験2-1 トランジスタの基本回路を実験する、加藤隆志
       
    
    

12. >関連項目

    1. エミッタ共通トランジスタ増幅回路(交流負帰還有り)
       

13. 実験の様子

    1. 自作電子ブロックの配置
       
       
       
    2. R_Eに使用した220Ω×5のブロック