エミッタ接地トランジスタ増幅回路(交流負帰還有り)の解析

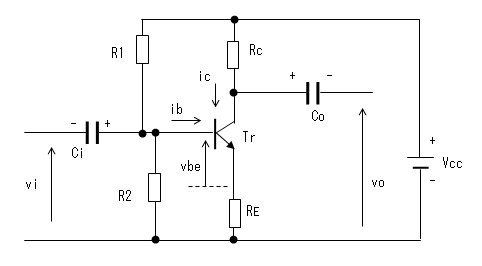
1. 回路図

   
   
   

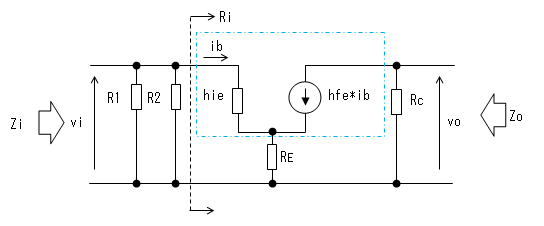
2. 増幅回路の等価回路

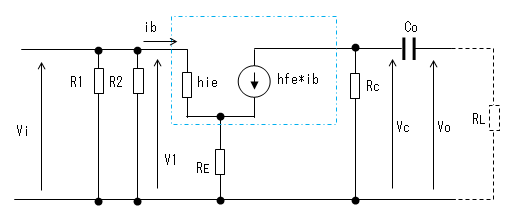
   増幅回路の等価回路は下図のようになります。
   トランジスタは エミッタ接地の小信号簡略化等価回路で置き換えます。
   電源のインピーダンスは零なので、電源Vccとグランド(GND)間は短絡します。
   また、2つのカップリング・コンデンサCiとCoは増幅する周波数帯域内では
   無視できる(=ゼロと見なせる)値を選定するため、CiとCoも短絡します。
   
   
   

3. 増幅回路の入力インピーダンスの計算

   まず、トランジスタのベースから右側を見たときの入力インピーダンスRiを求めます。
   等価回路から以下の関係式が成り立ちます。
   vi = ib * hie + R_E * (ib + hfe * ib) = ib * { hie + R_E * (hfe + 1)}
   
   従って、
   Ri = vi/ib = hie + R_E * (hfe + 1)
   
   このRiを使用すると、Ziは
   Zi = R1//R2//Ri
   　= R1 // R2 // [hie + R_E * (hfe + 1)]
   
   hfe = βなので
   Zi = R1 // R2 // [hie + R_E * (β + 1)]
   
   ここで、hieとして概算式を使うと、
   Zi　≒ R1 // R2 // [1/(40*I_B) + R_E * (β + 1)]
   　　＝ R1 // R2 // [β/(40*Ic) + R_E * (β + 1)]
   　　≒ R1 // R2 // [β/(40*I_E) + R_E * (β + 1)]
   
   また、 hie << R_E * (hfe + 1)と見なせるときは
   Ri = R_E * (hfe + 1) ≒ R_E * hfe　(∵　hfe >> 1)
   ∴　Ri ≒ R_E * hfe = R_E * β
   
   の式で概算出来ます。
   更に、R1//R2 << Riと見なして
   Zi = R1 // R2
   
   の式で概算しても実用になります。
   
   
   

4. 増幅回路の出力インピーダンスの計算

   制御電流源の内部抵抗は無限大であることに注目すると、 等価回路よりただちに、
   Zo = Rc
   
   (R_Eは関係しません。)
   
   
   

5. 増幅回路の電圧増幅度の計算

   まず、ibを求めます。
   ib = vi/Ri = vi/{hie + R_E * (hfe + 1)}
   
   一方、出力電圧voは
   vo = - ic * Rc
   　 = - (hfe * ib) * Rc
   　 = - hfe * [vi/{hie + R_E * (hfe + 1)}] * Rc
   ∴　vo = - vi * [hfe/{hie + R_E * (hfe + 1)}] * Rc
   
   ここで、マイナスの符号はvoがviに対して、
   位相が180度反転することを意味しています。
   以上より、電圧増幅度Avは
   Av = vo/vi
   ∴Av = - hfe/{hie + R_E * (hfe + 1)} * Rc ・・・・・�@
   
   なお、hieは概算式を使用すると、
   hie = β/(40 * Ic) = hfe/(40 * Ic)
   　　≒ β/(40 * I_E) = hfe/(40 * I_E)
   
   なので、hfe+1≒hfe(∵hfe>>1)、hfe=β、とすれば
   Av = - β/{β/(40 * Ic) + R_E * β} * Rc
   　 = - 1/{1/(40 * Ic) + R_E} * Rc
   ∴Av = - Rc/{1/(40 * Ic) + R_E}
   
   一方、�@の式において、hie >> R_E * (hfe + 1)、hfe+1 ≒ hfe
   一方、�@の式において、hie << R_E * (hfe + 1)、hfe+1 ≒ hfe
   であることを利用して近似すれば、
   vo = - vi * [hfe/{R_E * hfe}] * Rc
   　= - vi * [1/R_E] * Rc
   ∴vo = -vi * Rc/R_E
   
   となることから、
   Av = vo/vi = - Rc/R_E
   ∴Av =- Rc/R_E
   
   となり、抵抗器RcとR_EのみでAvが決まります。
   
   
   

6. 入力側カップリング・コンデンサCiの影響

   入力側カップリング・コンデンサCiの影響を検討します。
   出力側カップリング・コンデンサCoをこの後の項で検討するように
   無視出来る値(インピーダンス=0)に設定し、Ciのみを残すと
   等価回路は下図のようになります。
   一般的にはVi, V1, Voはフェーザ表示です。
   
   
   
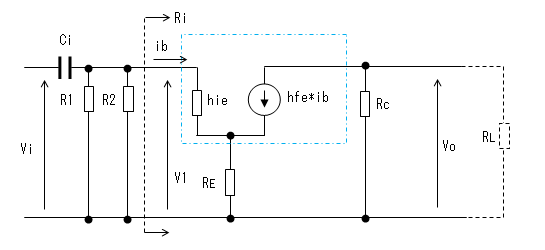
   トランジスタのベースから右側を見たときの入力インピーダンスをRiとすれば、
   R1、R2、Riは並列接続となるので、以下の計算においては
   Zi = R1 // R2 // Ri
   
   とします。
   ZiとCiはローカット・フィルタ(Low Cut Filter)を
   形成するため、周波数が低くなると減衰を無視できなくなります。
   
   
   
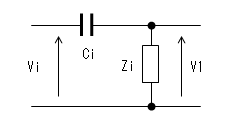
   この回路でカットオフ周波数をfciとすれば、ω=2π * fciなので
   fci = 1/(2π * Ci * Zi)
   
   となります。
   なお、信号源の内部抵抗(Rs)が無視できない場合、等価回路は下図となります。
   
   
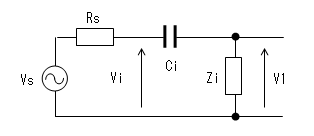
   この場合のカットオフ周波数をfciとすれば、ω=2π * fciなので
   fci = 1/{2π * Ci * (Rs + Zi)}
   
   となります。
   しかし、回路によってはRsの値が特定出来ない場合もあります。
   その場合、Rs=0[Ω]がワースト・ケースになるので、
   fci = 1/(2π * Ci * Zi)
   
   の式で計算すれば問題ないことになります。
   
   
   

7. 出力側カップリング・コンデンサCoの影響

   出力側カップリング・コンデンサCoの影響を検討します。
   入力側カップリング・コンデンサCiとエミッタのバイパス・コンデンサC_Eを
   この後の項で検討するように無視出来る値(インピーダンス=0)に設定し、
   Coのみを残すと等価回路は下図のようになります。
   
   
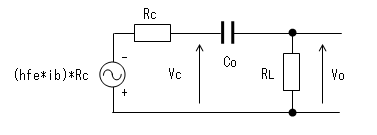
   制御電流源とコレクタ抵抗Rcとを ノートンの等価回路からテブナンの等価回路に
   変換すると下図のようになります。
   CoはRcと負荷抵抗R_Lとともにローカットフィルターを形成します。
   
   
   Coの値は、この増幅器の出力側のインピーダンスR_Lが
   決まらないと決められません。
   そのカットオフ周波数fcoとすれば、
   fco = 1/{2π * Co* (Rc + R_L)}
   
   となります。 また、Rc=0の方がワースト・ケースになるので、Rc＜R_LならCoを決める際
   fco = 1/(2π * Co* R_L)
   
   で計算するのも一案でしょう。
   
   
   

8. 参考文献