実験の目的
最も簡単な増幅回路であるトランジスタ一石からなるエミッタ接地増幅回路の実験を通じて、トランジスタによる電圧増幅作用を確認します。
実験にあたっては、小信号増幅を前提として、トランジスタを線形な素子として
近似して解析します。そして、この方法で求めた回路の増幅度と
入出力インピーダンスが、実験から得られた測定値と一致することを確認し、
回路設計の際に定量的な議論が出来るようにします。
実験課題
下記の項目について測定を行い、設計値と測定値を比較します。- 直流動作点
- 増幅度
- 入力インピーダンス
- 出力インピーダンス
実験回路
実験回路を下図に示します。出力側に接続した抵抗器:RLは、出力電圧の直流レベルを確定するために
接続しました。この抵抗がないと、電源投入時、出力コンデンサ:Coの電荷が0で
あるため、Coの両端の電圧が0となり、出力波形の直流レベルが浮き上がります。
交流信号に対してRL接続の影響が出ないように、RL >> Rcとなる
値を選定しました。

回路の動作
トランジスタに(近似的な)線形動作をさせるためには、まず バイアス電圧をかけ動作点を決めます。これは、入力電圧に交流を加えた場合、トランジスタの
動作範囲が能動領域 を逸脱しないようにするためです。
また、バイアス回路は電流帰還バイアス回路を用いており、
バイアス点を安定化しています。

入力信号はベースに印加 しますが、エミッタの抵抗REにはパスコンCEが
並列に接続されているため、エミッタは交流的にはグランドと同電位です。
そこで、入力信号Viを入力すると、
↓
Viはベース〜エミッタ間の電圧変化vbeとなる。
↓
ベース電流ibが変化する。
↓
コレクタ電流icがibのhfe(=β)倍されて変化する。
↓
icの変化がRcの両端の電圧Vcの変化となる。その値はvc = ic * Ro。
ここで、Ro = Rc//RL。
↓
vcの変化は出力voとして取り出される。
ちなみに、パスコンCEがあると交流的には負帰還がかかりません。
実験回路の設計
まず、直流動作点を決めるために、バイアス回路の設計をします。- 設計条件
-
(1)電源は乾電池1.5V×4本=6Vとします。
(2)コレクター電流:Ic=1mA
(3)エミッタ抵抗REの両端の電圧:VE=1V
(4)コレクタ抵抗Rcの両端の電圧:Vc=2.5V
(5)トランジスタは2SC1815のYランクを使う(データシートよりhFE=120〜240)
(6)増幅する周波数帯域の最低周波数は50Hz
(7)入力側(信号源)の出力インピーダンスは0[Ω] (実験では10[Ω])
(8)出力側(負荷)の入力インピーダンスは∞。(Co計算時は1kと仮定)

- バイアス回路の設計
-
(1)REの選定
REの両端の電圧VEを大きくする程、直流動作点が安定します。
しかしVEを大きくすると取り出せる出力電圧voの最大値が小さくなるため
最大出力電圧との兼ね合いで決めます。電源電圧Vccにもよりますが、
だいたい1〜3[V]くらいが相場(?)です。本実験ではVE = 1[V]とします。
RE = VE/IE ≒ VE/Ic = 1[V]/1[mA] = 1[kΩ]
∴RE = 1[kΩ]
(2)Rcの選定
Rcの両端の電圧Vcの目安は電源電圧Vccからエミッタ抵抗REの両端の電圧VEを
引いた値の1/2です。本実験ではVcc = 6.0[V]、VE = 1[V]としたので
Vc = (6 - 1)/2 = 2.5[V]位が目安ですが、交流信号の最大出力の振幅が大きく
なければそれほど神経質に設定する必要はありません。
Rc = Vc/Ic = 2.5[V]/1[mA] = 2.5[kΩ]
実際には、E-6系列より選定し、
Rc = 2. 2[kΩ]としました。
(3)R1、R2の選定
VBEを0.7[V]とすると、VE=1[V]としたので、R2の両端の電圧V1は
1.7[V]となります。
一方、R1、R2に流すブリーダー電流はIBの約10倍に設定します。
トランジスタのhFEはデータシートよりhFE(min)=120なので
(ベース電流が最も大きくなる条件で考えた)
IB = Ic/hFE = 1[mA]/120 = 8.3[μA]
なので、ブリーダ電流をIBの10倍の83[μA]とすれば、
R1 + R2 = Vcc/(ブリーダ電流) = 6[V]/83[μA] = 72[kΩ]
よって、 R2 = 1.7[V]/6[V] * 72[kΩ] = 20.4[kΩ]
R1 = 72[kΩ] - 20.4[kΩ] = 51.6[kΩ]
実際には、E-6系列より選定し、
R1 = 47[kΩ]
R2 = 22[kΩ]
としました。
以上より決定した定数から、改めて各部の電圧・電流を計算すると、
V1 = R2/(R1 + R2) * Vcc = 22[kΩ]/(47[kΩ] + 22[kΩ]) * 6[V] ≒ 1.9[V]
VE = V2 - VBE = 1.9[V] - 0.7[V] = 1.2[V]
IE = VBE/RE = 1.2[V]/1[kΩ] = 1.2[mA]
Ic ≒ IE = 1.2[mA]
Vc = Rc * Ic = 2.2[kΩ] * 1.2[mA] ≒ 2.6[V]
VCE = Vcc - Vc - VE = 6 - 2.6 - 1.2 = 2.2[V]

- 増幅回路の等価回路
-
交流の等価回路ではカップリング・コンデンサのCi、Coとバイパス・コンデンサのCEは
短絡して考えます。増幅する周波数帯ではコンデンサのリアクタンスが十分小さく
なるように値を決めるため、交流的には短絡して考えるのですが、
その値を決めるためには、入力インピーダンスの計算が必要なので、
手順が前後するように見えますが、まず、増幅回路の等価回路から
3個のコンデンサCi、Co、CEを短絡した下図の等価回路で考えます。
トランジスタはエミッタ接地の 小信号簡略等価回路に置き換え、
また、Vccとグランド(GND)も交流的には同電位なので接続してあります。

計算にあたってhieの値が必要になりますが、 概算式である
hie = β/(40 * Ic)
の式を用います。
バイアス回路の設計の項で記述したように、今回の実験回路では、Ic =1.2[mA]です。
また、本実験に使用するトランジスタのβは 静特性の測定実験で測定した値を
使用すると175になりますので
hie = β/(40 * Ic) = 175/(40 * 0.0012)
∴hie=3646[Ω]
となります。
- 入力インピーダンスの計算
-
等価回路より、入力インピーダンスはR1、R2、hieが並列接続されていますので、
Zi = R1//R2//hie
となります。
まず、RB = R1//R2として、RBを計算すると、
RB = (47k * 22k)/(47k + 22k) = 14.985・・・ ≒ 15[kΩ]
従って、
Zi = RB//hie =15000 // 3646[Ω]
∴Zi ≒ 2933[Ω]
となります。
- 出力インピーダンスの計算
-
制御電流源のインピーダンスは無限大であるため、等価回路より、
Zo = Rc = 2200[Ω]
となります。
- 増幅度の計算
-
hieの概算式は、
hie = β/(40×Ic)
でしたので、hfe=βとして、電圧増幅度Avは
Av = - (hfe/hie) * Rc = - β /[β/(40×Ic)] * Rc = - 40 * Ic * Rc = - 40 * 0.0012 * 2200
∴Av = -106[倍]
となります。
- コンデンサの容量の決定
-
(1)実験回路の等価回路
ここでは、Ci、Co、CEの値を検討するため、それぞれ省略しない状態の
等価回路を考えます。
トランジスタをエミッタ接地の 小信号簡略等価回路に置き換え、
また、VccとGNDは交流的には同電位であることから接続してしまうと
実験回路の小信号等価回路は下図のようになります。

(2)入力コンデンサ(Ci)
入力コンデンサCiの影響がないように定数を決定します。
R1、R2、hieの並列回路の合成抵抗をRとします。すなわち
R = R1//R2//hie
とすれば、RとCiはローカット・フィルター(Low Cut Filer)を構成するため
Ciの値が小さいと増幅する周波数帯域の低域側で増幅度が
低下してしまいます。この影響をなくすためには、
フィルタのカットオフ周波数が信号の最低周波数より
十分小さくなるようにCiを決定します。

このローカット・フィルターのカットオフ周波数fciは、
fci = 1/(2π * Ci * R)
となりますので、信号の最低周波数をfslとすれば
fsl >> fci
となるようにCiを決定すればよいことになります。よって
fsl >> 1/(2π * Ci * R)
∴Ci >> 1/(2π * fsl * R)
入力信号の最低周波数(fsl)を50[Hz]とします。
Rの値は入力インピーダンスの項で計算したように(Ziとして計算した)
R = 2933[Ω]
でしたので、
Ci >> 1/(2π * fsl * R) = 1/(2π * 50 * 2933) ≒ 1.09[μF]
電解コンデンサは経年変化により静電容量が減少しますので、
少なくとも計算値の2倍は欲しいところです。
今回は、計算値より大き目の10[μF]とします。
(3)出力コンデンサ(Co) ---(2024/09/28 修正)
出力コンデンサCoの影響がないように定数を決定します。
本増幅回路の次段の回路の入力抵抗:RLとすれば、
RcとRLとCoはローカット・フィルター(Low Cut Filer)を構成するため
Coの値が小さいと増幅する周波数帯域の低域側で増幅度が
低下してしまいます。この影響をなくすためには、
フィルタのカットオフ周波数が信号の最低周波数より
十分小さくなるようにCoを決定します。
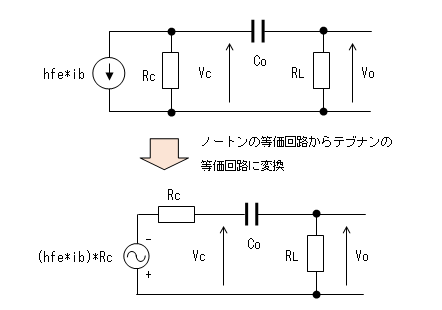
(ノートンの等価回路からテブナンの等価回路への変換は こちら。)
このローカット・フィルターのカットオフ周波数fcoは、
fco = 1/(2π * Co * RL)
fco = 1/{2π * Co * (Rc + RL)}
となりますので、信号の最低周波数をfslとすれば
fsl >> fco
となるようにCoを決定すればよいことになります。よって
fsl >> 1/(2π * Co * RL)
∴ Co >> 1/(2π * fsl * RL)
fsl >> 1/{2π * Co * (Rc + RL)}
∴ Co >> 1/{2π * fsl * (Rc + RL)}
入力信号の最低周波数(fsl)を50[Hz]とします。
RL=1[kΩ](実験の際のRLとは値が異なる)と仮定して、計算すると
Co >> 1/(2π * fsl * R) = 1/(2π * 50 * 1000) ≒ 3.18[μF]
Co >> 1/{2π * fsl * (Rc + RL)} = 1/{2π * 50 * (2200 + 1000)} ≒ 0.99[μF]
電解コンデンサは経年変化により静電容量が減少しますので、
少なくとも計算値の2倍は欲しいところです。
今回は、計算値より大き目の22[μF]とします。
(4)エミッタ・バイパス・コンデンサ(CE)
バイパス・コンデンサCEの影響がないように定数を決定します。
トランジスタのhieとCEはローカット・フィルター(Low Cut Filer)を構成するため
CEの値が小さいと増幅する周波数帯域の低域側で増幅度が
低下してしまいます。この影響をなくすためには、
フィルタのカットオフ周波数が信号の最低周波数より
十分小さくなるようにCEを決定します。
このローカット・フィルターのカットオフ周波数fceは、
fce = 20 * Ic /[π * CE]
となりますので、信号の最低周波数をfslとすれば
fsl >> fce
となるようにCiを決定すればよいことになります。よって
fsl >> fce = 20 * Ic /[π * CE]
∴CE >> 20 * Ic /{π * fsl}
入力信号の最低周波数を(fsl)50[Hz]とします。
Icは1.2[mA]としましので CE >> 20 * 0.0012 /[π * 50] ≒ 153[μF]
となり、かなり大きな容量が必要となることが判ります。
電解コンデンサは経年変化により静電容量が減少しますので、
少なくとも計算値の2倍は欲しいところです。
本実験では、CE = 470[μF]としました。
実験方法
-
信号源としては、トランス・ボックス
を使用します。
従って、周波数は(東日本では)50Hzになります。
トランス・ボックスの出力電圧がそのままでは電圧が高過ぎるので
33kΩと10Ωの抵抗器により分圧し、2mV(rms)程度まで減衰させます。
このとき、アッテネータとしてグランドとの間に10Ωを使用すると
増幅器からみたときの信号源のインピーダンスが10Ωと低く
抑えられるので、実験には好都合です。

測定には5kΩの可変抵抗器 とディジタル・テスターの交流電圧測定機能を使用して、
簡易測定法により、電圧増幅度、入力インピーダンス、出力インピーダンスを
それぞれ測定します。
- 電子ブロックの配置

- 直流動作点の測定
ディジタルテスターの直流電圧測定レンジで、下図に示すようにVc、VCE、VE、
V1、VBEを測定します。IcはVcとRcの値からIc=Vc/Rcの式により求めます。
また、電源電圧も正確に6.0[V]ではないので、測定しておきます。

- 電圧増幅度の測定
増幅回路における電圧増幅度の簡易測定法によります。
(1)下図の測定回路を組立てます。

(2)vsの値を読みます。
(3)voの値を読みます。
(4)vsの値に減衰回路の減衰比をかけてviを求めます。
今回の回路では、減衰比は10/33010になります。
(5)viの値とvoの値から電圧増幅度Av=vo/viを求めます。
- 入力インピーダンスの測定
増幅回路における入力インピーダンスの簡易測定法によります。
(1)下図の測定回路を組立てます。

(2)VRを0[Ω]の状態にしてvoの値を読み取ります。
この時のvoの読みをvo0とします。
(3)voの値が1/2*vo0となるようにVRを調整します。
(4)VRを回路から外し、テスターの抵抗レンジでVRの値を読み取ります。
この時のVRの値がZiとなります。
- 出力インピーダンスの測定
増幅回路における出力インピーダンスの簡易測定法によります。
(1)下図の測定回路を組立てます。

(2)SWを開放の状態にしてvoの値を読み取ります。
この時のvoの読みをvo0とします。
(3)SWを閉じて(短絡)からvoの値が1/2*vo0となるようにVRを調整します。
(4)VRを回路から外し、テスターの抵抗レンジでVRの値を読み取ります。
この時のVRの値がZoとなります。
なお、SWについては、実際は配線を取り外すことにより解放しました。
実験機材
- 電子ブロック
-
使用したブロックは、実験方法の
電子ブロックの配置を参照。
- トランス・ボックス
- 5kΩの可変抵抗器
- 固定抵抗器:33kΩ(1%)、10Ω(1%)
- ディジタル・テスター
- 乾電池:1.5V×4本、乾電池ホルダー
- 配線材
実験結果
- 直流動作点の測定
下図に測定結果を示します。
白色の吹き出しで計算値、黄色の吹き出しで測定値を表しました。

- 電圧増幅度の測定
viの値は、vsの値に減衰比=10/33010をかけて算出しました。
vsの値 [V] viの値 [mV] voの値 [mV] 備考 6.70 2.03 206 282vo訂正(2024/9/10)
以上の測定結果より、電圧増幅度Avを計算すると、
Av = vo/vi = 282/2.03
Av = vo/vi = 206/2.03 ← 訂正(2024/09/10)
∴ Av = 102← 計算合わない。(T_T)
Av(絶対値)の計算値と測定値を比較すると、
Av (計算値) Av (測定値) 測定値/計算値 (%) 備考 106 102 -3.8
- 入力インピーダンスの測定
VRの値 [Ω] voの値 [V] 備考 0 0.206 voのこの値がvo0 3202 0.103 (vo=1/2 * vo0)
以上の測定結果より、
Zi = 3202[Ω]
Ziの計算値と測定値を比較すると、
Zi (計算値) [Ω] Zi (測定値) [Ω] 測定値/計算値 (%) 備考 2933 3202 9.2
- 出力インピーダンスの測定
VRの値 [Ω] voの値 [V] 備考 ∞ (SW:開放) 0.206 voのこの値がvo0 2152 (SW:短絡) 0.103 (vo=1/2 * vo0)
以上の測定結果より、
Zo = 2152[Ω]
Zoの計算値と測定値を比較すると、
Zo (計算値) [Ω] Zo (測定値) [Ω] 測定値/計算値 (%) 備考 2200 2152 -2.2 抵抗器の誤差(1%)は含まない
測定結果・考察
-
下記のいずれの項目も、設計値と測定値は概ね一致しました。
- 直流動作点
- 増幅度
- 入力インピーダンス
- 出力インピーダンス
今後の課題
- 周波数特性の測定
周波数特性は増幅回路の基本的な特性のひとつですが、今回の実験では
信号源として発振器ではなく、トランス・ボックスを使用する方針としたので
周波数特性の測定は断念しました。
- ひずみ率の測定
用途によってはひずみ率も重要な特性ですが、ひずみ率計が手元にないため
将来の課題としました。
参考文献
- 実験で学ぶ最新トランジスタ・アンプ設計法(1988 4版)、黒田徹著、ラジオ技術社
関連項目
実験中の様子
- 自作電子ブロックの配置

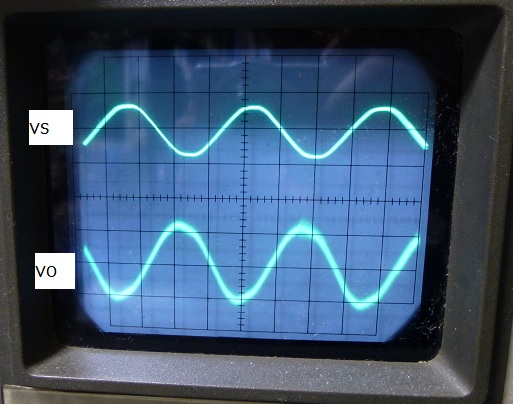
- 入出力波形
vsとvoの波形。位相が180度反転している。
(配線が長いせいか、voの波形は少しにじんでいるが・・・・。)
- 測定中の様子
