エミッタ接地小信号増幅回路(交流負帰還なし)の解析

1. 回路図

   
   
   

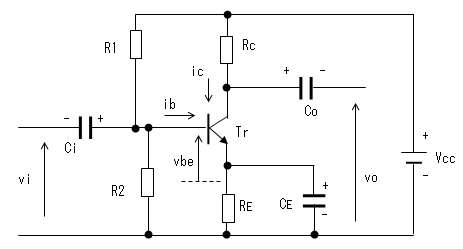
2. 増幅回路の等価回路

   エミッタ接地小信号増幅回路の等価回路を求めると下図となります。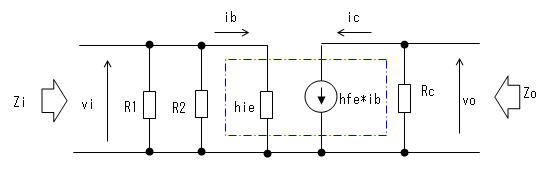
   
   
   

3. 増幅回路の入力インピーダンスの計算

   等価回路から、回路の入力インピーダンス(Zi)を求めます。
   Zi = R1 // R2 // hie
   
   ここで、//は並列接続の記号で、Ra//Rb = Ra*Rb/(Ra + Rb)の意味です。
   
   hieは概算式を用いると、
   Zi　≒ R1 // R2 // [1/(40*I_B)]
   　　＝ R1 // R2 // [β/(40*Ic)]
   　　≒ R1 // R2 // [β/(40*I_E)]
   
   

4. 増幅回路の出力インピーダンスの計算

   
   
   同様に等価回路から、回路の出力インピーダンス(Zo)を求めます。
   電流源の内部抵抗は無限大であることに注目すると、
   Zo = Rc
   
   
   

5. 増幅回路の電圧増幅度の計算

   
   
   等価回路から、電圧増幅度を計算します。
   まず、ibを求めます。
   ib = vi/hie
   
   一方、出力電圧voは
   vo = - ic * Rc
   　 = - (hfe * ib) * Rc
   　 = - hfe * (vi/hie) * Rc
   ∴vo = - vi * (hfe/hie) * Rc
   
   ここで、マイナスの符号はvoがviに対して、
   位相が180度反転することを意味しています。
   以上より、電圧増幅度Avは
   Av = vo/vi
   ∴Av = - (hfe/hie) * Rc
   
   なお、hieは概算式を使用すると、
   hie = β/(40 * Ic) = hfe/(40 * Ic)
   　　≒ β/(40 * I_E) = hfe/(40 * I_E)
   
   なので、β=hfeとおいて
   Av = - β / [β/(40 * Ic)] * Rc
   ∴Av = - 40 * Ic * Rc
   
   
   

6. 入力側カップリング・コンデンサCiの影響

   入力側カップリング・コンデンサCiの影響を検討します。
   出力側カップリング・コンデンサCoとエミッタのバイパス・コンデンサC_Eを
   この後の項で検討するように無視出来る値(インピーダンス=0)に設定し、
   Ciのみを残すと等価回路は下図のようになります。
   一般的にはVi, V1, Voはフェーザ表示です。
   
   
   
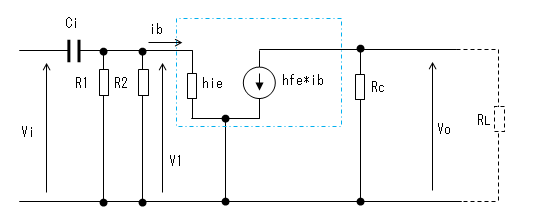
   まず、R1、R2、hieは並列接続になるので、以下の計算においては
   R_B = R1//R2 = R1*R2/(R1+R2)
   Zi = R_B//hie = R_B*hie/(R_B+hie)
   とします。
   
   ZiとCiはローカット・フィルタ(Low Cut Filter)を
   形成するため、周波数が低くなると減衰を無視できなくなります。
   
   
   
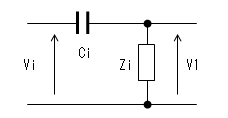
   この回路でカットオフ周波数をfciとすれば、ω=2π * fciなので
   fci = 1/(2π * Ci * Zi)
   
   となります。
   なお、信号源の内部抵抗(Rs)が無視できない場合、等価回路は下図となります。
   
   
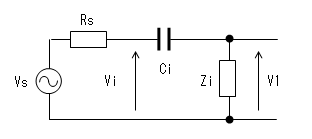
   この場合のカットオフ周波数をfciとすれば、ω=2π * fciなので
   fci = 1/{2π * Ci * (Rs + Zi)}
   
   となります。
   しかし、回路によってはRsの値が特定出来ない場合もあります。
   その場合、Rs=0[Ω]がワースト・ケースになるので、
   fci = 1/(2π * Ci * Zi)
   
   の式で計算すれば問題ないことになります。
   

7. 出力側カップリング・コンデンサCoの影響

   出力側カップリング・コンデンサCoの影響を検討します。
   入力側カップリング・コンデンサCiとエミッタのバイパス・コンデンサC_Eを
   この後の項で検討するように無視出来る値(インピーダンス=0)に設定し、
   Coのみを残すと等価回路は下図のようになります。
   一般的にVc、Voなどはフェーザ表示です。
   
   
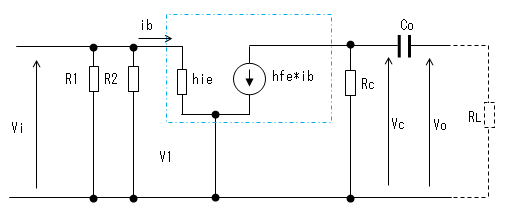
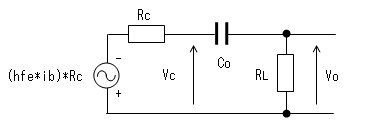
   制御電流源とコレクタ抵抗Rcとを ノートンの等価回路からテブナンの等価回路に
   変換すると下図のようになります。
   CoはRcと負荷抵抗R_Lとともにローカットフィルターを形成します。
   
   
   Coの値は、この増幅器の出力側のインピーダンスR_Lが
   決まらないと決められません。
   そのカットオフ周波数をfcoとすれば、
   fco = 1/{2π * Co * (Rc + R_L)}
   
   となります。
   また、Rc=0の方がワースト・ケースになるので、Rc＜R_LならCoを決める際
   fco = 1/(2π * Co* R_L)
   
   で計算するのも一案でしょう。
   

8. バイパス・コンデンサC_Eの影響

   まず、CiとCoの影響がないように値を決定します。
   更に、R_Eと並列に接続されているバイパスコンデンサC_Eの値を
   R_Eの影響がなくなるように
   R_E >> 1/(ωC_E)
   となるよう決定すれば、等価回路は次のように簡略化されます。
   
   
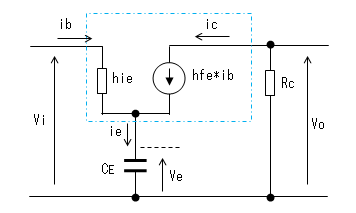
   等価回路によりベースより流入する交流電流はib、
   コレクタより流入する交流電流icは
   ic = hfe * ib
   となるので、エミッタより流出する交流電流ieは
   ie = ib + ic = ib + hfe*ib = ib * (1 + hfe) となります。
   従って、エミッタの交流電位Veは
   Ve = 1/(jωC_E) * ie
   = 1/(jωC_E) * ib * (1 + hfe)
   = (hfe + 1)/(jωC_E) * ib
   これにより
   Vi = ib * hie + Ve
   = ib * hie + (hfe + 1)/(jωC_E) * ib
   = ib * {hie + (hfe + 1)/(jωC_E)}
   = ib * {hie + 1/[jω{C_E/(hfe + 1)}]
   ≒ ib * {hie + 1/[jω(C_E/hfe)]　　(∵　hfe>>1)
   この式は、次の等価回路と同じです。
   
   
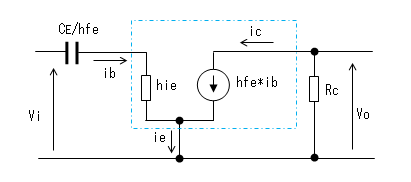
   すなわち、入力側からみた場合C_Eは1/hfe倍に見え、
   hieとC_E/hfeとでローカットフィルタを形成しています。
   (Viとibとの関係なので、C_E/hfeとhieを入れ換えても
   ローカットフィルタであることには変わりありません。
   本ページ最下部の付録を参照してください。)
   
   よって、そのカットオフ周波数fceは、
   fce = hfe/{2π * C_E * hie}
   
   ここで、hieに概算式を用いると、β=hfeとして
   fce = β/[2π * C_E * {β/(40 * Ic)}]
   ∴fce = 20 * Ic /[π * C_E]
   
   となります。
   
   
   

9. 参考文献

   1. 簡明電子回路入門(1980 初版)、矢部初男著、槇書店
      
   2. アナログ電子回路の基礎(2003 第1版第1刷)、堀桂太郎、東京電機大学出版局

10. 付録

    ib = Vi/[hie + 1/{jωC_E/hfe}]
    |ib| = |Vi|/[√{hie² + 1/(ωC_E/hfe)²}]
    
    ω→∞のとき
    lim_ω→∞|ib| = |Vi|/hie
    
    カットオフ周波数fcは
    (lim_ω→∞|ib|)/√2 = |ib|
    
    となる周波数なので、以下計算すると
    |Vi|/(hie * √2) = |Vi|/[√{hie² + 1/(ωC_E/hfe)²}]
    
    両辺を|Vi|で割ってから、分母をはらうと
    √{hie² + 1/(ωC_E/hfe)²} = √2 * hie
    
    両辺を自乗して
    hie² + 1/(ωC_E/hfe)² = 2 * hie²
    1/(ωC_E/hfe)² = hie²
    
    両辺の平方根をとって
    1/(ωC_E/hfe) = hie
    ω = 1/(C_E/hfe * hie)
    
    ω = 2π*fcとすれば
    fc = 1/[2π * (C_E/hfe) * hie]