2端子対回路　(Y、Z、Hパラメータ)

1. 2端子対回路

電子回路では、回路網をブラック・ボックスとみなし、入力端子対と出力端子対との
2対からなる2端子対回路(4端子回路とも言う)として扱うことをしばしば
行います。2端子対回路の一般論は電気回路学で学びますが、
入力電圧・入力電流・出力電圧・出力電流の関係を2×2の行列で表現します。
ここではY行列、Z行列、H行列について記載します。
(行列の代わりにパラメータと呼ぶこともあります。)



2. Yパラメータ

2端子対を持つ線形回路の端子1-1'に電源E₁を、端子2-2'に電源E₂を
接続した状態を考えます。
端子1-1'間の電圧をV₁、端子1に流れ込む電流をI₁
端子2-2'間の電圧をV₂、端子1に流れ込む電流をI₂
とします。ここで、E₁、E₂、V₁、 I₁、V₂、I₂は、一般的には
フェーザ表示です。


回路全体が線形なので、重ね合わせの理を使って、I₁、I₂ を求めます。

まず、E₂ = 0としたとき、端子1に流れる電流をI₁'
端子2に流れる電流をI₂'とすれば、I₁'、I₂'は V₁に比例するので、
比例定数をY₁₁、Y₂₁として下記の式が成り立ちます。
I₁' = Y₁₁ * V₁
I₂' = Y₂₁ * V₁


次に、E₁ = 0としたとき、端子1に流れる電流をI₁"
端子2に流れる電流をI₂"とすれば、I₁"、I₂"は V₂に比例するので、
比例定数をY₁₂、Y₂₂として下記の式が成り立ちます。
I₁" = Y₁₂ * V₂
I₂" = Y₂₂ * V₂


E₁とE₂が同時に存在したときの電流、I₁、 I₂は
重ね合わせの理により下記の式となります。
I₁ = I₁' + I₁" = Y₁₁ * V₁ + Y₁₂ * V₂
I₂ = I₂' + I₂" = Y₂₁ * V₁ + Y₂₂ * V₂

これを行列の式で表すと、


Y₁₁、 Y₁₂、Y₂₁、Y₂₂は電圧に かけると電流になる比例定数なので、
アドミタンスになります。
そして2×2型の行列YをYパラメータと呼びます。


Yパラメータが純抵抗(コンダクタンス)の場合は小文字を用います。




3. Yパラメータの等価回路

yパラメータが与えられると
i₁ = y₁₁ * v₁ + y₁₂ * v₂ 　・・・・・　�@
i₂ = y₂₁ * v₁ + y₂₂ * v₂ 　・・・・・　�A

の式が成り立ちます。ここではYパラメータは純抵抗として小文字で表しています。
この式から等価回路を導きます。
�@式より電流i₁は、電流(y₁₁ * v₁)と 電流(y₁₂ * v₂)の和です。
�@式の第1項(y₁₁ * v₁)は電圧v₁に アドミタンスY₁₁[S]
の抵抗(つまり抵抗値は1/y₁₁[Ω])を接続したときに流れる電流ですので、
下図のように1-1'端子間に接続した抵抗y₁₁[S]で表すことが出来ます。
第2項は、2次側の電圧V₂に比例した 制御電流源とします。


�A式より2次側の電流i₂についても同様に考えると、yパラメータの
等価回路は一応下図で表せます。


しかし、この等価回路は1次側と2次側が分離していて使いずらいので、
以下の手順で変形します。

まず、�@式の第2項を変形します。
y₁₂ * v₂ = -y₁₂ * (v₁ - v₂) + y₁₂ * v₁

この式の第1項は、下図のようにa点とb点との間にアドミタンス-y₁₂を
挿入したときa→bに流れる電流です。


第2項は、y₁₁と並列に接続した抵抗y₁₂[S]で表すことが出来ます。
式の変形により、1次側の制御電流源 は、下図のようにふたつの抵抗に変形する
ことが出来ます。a-b間の抵抗y₁₂にはマイナスがつきますが、これはy₁₂自体が
マイナスなので、マイナスをつけることでプラスになるからです。


次に2次側を変形します。�A式の第1項を以下のように変形します。
1次側の等価回路の変形により、b点から-y₁₂ * (v₁ - v₂) の電流が
流れ込んでくることを考慮して、
(下図では、a-b間の電圧の極性の取り方を逆にしていることに注意)
y₂₁ * v₁ = -y₁₂ * (v₂ - v₁) + (y₂₁ - y₁₂) * v₁ + y₁₂ * v₂

この式の第1項は-y₁₂をb→aに流れる電流、第2項は 制御電流源に置換え、
第3項は、y₂₂と並列に接続した抵抗y₁₂[S]で表すことが出来ます。


以上の変形から、下図の等価回路が得られます。
これをYパラメータにおけるπ(パイ)型等価回路といいます。
(抵抗はアドミタンス表示なので、並列接続の合成抵抗は加算となります。念のため)




4. Zパラメータ



2端子対回路において
V₁、V₂を従属変数、I₁、I₂を独立変数 としたとき、
Z₁₁、 Z₁₂、Z₂₁、Z₂₂を比例定数として
下記の式でV₁、V₂を表します。
V₁ = Z₁₁ * I₁ + Z₁₂ * I₂
V₂ = Z₂₁ * I₁ + Z₂₂ * I₂

これを行列の式で表すと、


Z₁₁、 Z₁₂、Z₂₁、Z₂₂は電流に かけると電圧になる比例定数なので、
インピーダンスになります。
そして2×2型の行列ZをZパラメータと呼びます。


Zパラメータが純抵抗の場合は小文字を用います。




5. Zパラメータの等価回路

zパラメータが与えられると
v₁ = z₁₁ * i₁ + z₁₂ * i₂ 　・・・・・　�B
v₂ = z₂₁ * i₁ + z₂₂ * i₂ 　・・・・・　�C

の式が成り立ちます。ここではZパラメータは純抵抗として小文字で表しています。
この式からただちに下記の等価回路が導けます。


しかし、この等価回路も1次側と2次側が分離していて使いずらいので、
以下の手順で変形します。方針としては下図のように(i₁+i₂)
の項を生成するように変形します。


まず、�B式の第2項を変形します。
z₁₂ * i₂ = z₁₂ * (i₁ + i₂) - z₁₂ * i₁
この式の第1項は抵抗z₁₂に電流(i₁+i₂)が流れたときの 電圧を表します。
第2項は抵抗-z₁₂に電流i₁が流れたときの電圧を表しますので、
1次側の電圧源は下図のように表せます。


次に、�C式の第1項を変形します。
z₂₁ * i₁ = z₁₂ * (i₁ + i₂) + (z₂₁ - z₁₂) * i₁ - z₁₂ * i₂
この式の第1項は抵抗z₁₂に電流(i₁+i₂)が流れたときの 電圧を表します。
第2項は比例定数が(z₂₁-z₁₂)で電流i₁に比例する
制御電圧源 とします。第3項はz₂₂と直列になる抵抗の両端の電圧となります。
以上より、2次側の電圧源は下図のように表せます。


以上の変形から、下図の等価回路が得られます。
これをZパラメータにおけるT型等価回路といいます。




6. Hパラメータ



2端子対回路において
V₁、I₂を従属変数、I₁、V₂を独立変数 としたとき、
H₁₁、 H₁₂、H₂₁、H₂₂を比例定数として
下記の式でV₁、I₂を表します。
V₁ = H₁₁ * I₁ + H₁₂ * V₂
I₂ = H₂₁ * I₁ + H₂₂ * V₂

何とも覚えずらい式で往生してしまいますが(笑)、バイポーラ・トランジスタを
等価回路で表現するとき、Hパラメータがもっともトランジスタの特徴を表します。
(バイポーラ・トランジスタを使うとき、いやでも覚えてしまいます。笑)
これを行列の式で表すと、


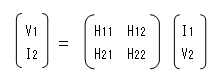
H₁₁はインピーダンス、 H₁₂は無名数、
H₂₁は無名数、H₂₂はアドミタンスになります。
そして2×2型の行列HをHパラメータと呼びます。


フェーザ表示する必要がない場合は小文字を用います。




7. Hパラメータの等価回路

hパラメータが与えられると
v₁ = h₁₁ * i₁ + h₁₂ * v₂ 　・・・・・　�D
i₂ = h₂₁ * i₁ + h₂₂ * v₂ 　・・・・・　�E

の式が成り立ちます。ここではHパラメータは純抵抗として小文字で表しています。

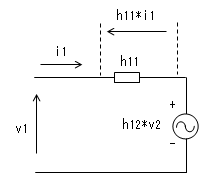
�D式より、v₁は(h₁₁ * i₁)と(h₁₂ * v₂)の 電圧の和です。
第1項の(h₁₁ * i₁)は、抵抗h₁₁に電流i₁が流れたときの
抵抗h₁₁の両端の電圧を表します。
第2項の(h₁₂ * v₂)は、h₁₂を比例定数とするv₂による 制御電圧源とします。


�E式より、i₂は(h₂₁ * i₁)と(h₂₂ * v₂)の 電流の和です。
第1項の(h₂₁ * i₁)はh₂₁を比例定数とするv₁による 制御電流源とします。
第2項の(h₂₂ * v₂)はコンダクタンスh₂₂に電圧 v₂を
印加したときh₂₂に流れる電流を表しています。


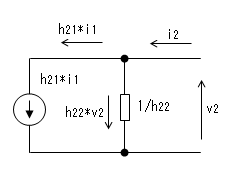
以上より、下記に示すhパラメータの等価回路が導けます。




8. 参考文献

1. 簡明電子回路入門(1980 初版) 第4章 4端子回路理論、矢部初男著、槇書店



9. パラメータの相互変換(計算式)

計算の手順は、
(1)変換前のパラメータから式を作る
(2)変換前後の独立変数と従属変数を意識しながら式を変形する。
(3)変換後の式の形になったら、係数から変換式を取り出す。
と、言ったところです。


1. ZパラメータからYパラメータへの変換
Zパラメータの式は下記でした。
v₁ = z₁₁ * i₁ + z₁₂ * i₂ 　・・・・・　(1)
v₂ = z₂₁ * i₁ + z₂₂ * i₂ 　・・・・・　(2)

Yパラメータの従属変数はi₁、i₂なので、ここではi₂を 消去するために
(1)式にz₂₂をかけ、(2)式にz₁₂をかけて辺々引きます。
z₂₂ * v₁ - z₁₂ * v₂ = (z₁₁ * z₂₂ - z₁₂ * z₂₁) * i₁

�凛 = z₁₁ * z₂₂ - z₁₂ * z₂₁と 置換えて、i₁の式に変形すると
i₁ = (z₂₂ / �凛) * v₁ - (z₁₂ / �凛) * v₂

Yパラメータの式と比較すると
y₁₁ = z₂₂ / �凛
y₁₂ = -z₁₂ / �凛

を得ます。次に、i₁を消去するため
(1)式にz₂₁をかけ、(2)式にz₁₁をかけて辺々引きます。
z₁₂ * v₁ - z₁₁ * v₂ = -(z₁₁ * z₂₂ - z₁₂ * z₂₁) * i₂

�凛 = z₁₁ * z₂₂ - z₁₂ * z₂₁と 置換えて、i₂の式に変形すると
i₂ = -(z₁₂ / �凛) * v₁ + (z₁₁ / �凛) * v₂

Yパラメータの式と比較すると
y₂₁ = -z₁₂ / �凛
y₂₂ = z₁₁ / �凛

を得ます。


2. HパラメータからYパラメータへの変換
Hパラメータの式は下記でした。
v₁ = h₁₁ * i₁ + h₁₂ * v₂ 　・・・・・　(3)
i₂ = h₂₁ * i₁ + h₂₂ * v₂ 　・・・・・　(4)

Yパラメータの従属変数はi₁、i₂ですが、(3)式を変形すると
ただちにi₁の式が得られます。
i₁ = 1 / h₁₁ * v₁ - (h₁₂ / h₁₁) * v₂ 　・・・・・　(3')

Yパラメータの式と比較すると
y₁₁ = 1 / h₁₁
y₁₂ = -h₁₂ / h₁₁

を得ます。次に、i₁を消去するため(3')式を(4)式に代入します。
i₂ = h₂₁ * {1 / h₁₁ * v₁ - (h₁₂ / h₁₁) * v₂} + h₂₂ * v₂
　= (h₂₁ / h₁₁) * v₁ - (h₁₂ * h₂₁ / h₁₁) * v₂ + h₂₂ * v₂
　= (h₂₁ / h₁₁) * v₁ + {(h₁₁ * h₂₂ - h₁₂ * h₂₁) / h₁₁)} * v₂

�冑 = h₁₁ * h₂₂ - h₁₂ * h₂₁と 置換えると
i₂ = (h₂₁ / h₁₁) * v₁ - (�冑 / h₁₁) * v₂

Yパラメータの式と比較すると
y₂₁ = h₂₁ / h₁₁
y₂₂ = �冑 / h₁₁

を得ます。


3. YパラメータからZパラメータへの変換
Yパラメータの式は下記でした。
i₁ = y₁₁ * v₁ + y₁₂ * v₂ 　・・・・・　(5)
i₂ = y₂₁ * v₁ + y₂₂ * v₂ 　・・・・・　(6)

Zパラメータの従属変数はv₁、v₂なので、ここではv₂を 消去するために
(5)式にy₂₂をかけ、(6)式にy₁₂をかけて辺々引きます。
y₂₂ * i₁ - y₁₂ * i₂ = (y₁₁ * y₂₂ - y₁₂ * y₂₁) * v₁

�凉 = y₁₁ * y₂₂ - y₁₂ * y₂₁と 置換えて、v₁の式に変形すると
v₁ = (y₂₂ / �凉) * i₁ - (y₁₂ / �凉) * i₂

Zパラメータの式と比較すると
z₁₁ = y₂₂ / �凉
z₁₂ = -y₁₂ / �凉

を得ます。次に、v₁を消去するため
(5)式にy₂₁をかけ、(6)式にy₁₁をかけて辺々引きます。
y₂₁ * i₁ - y₁₁ * i₂ = -(y₁₁ * y₂₂ - y₁₂ * y₂₁) * v₂

�凉 = y₁₁ * y₂₂ - y₁₂ * y₂₁と 置換えて、v₂の式に変形すると
v₂ = -(y₂₁ / �凉) * i₁ + (y₁₁ / �凉) * i₂

Zパラメータの式と比較すると
z₂₁ = -y₂₁ / �凉
z₂₂ = y₁₁ / �凉

を得ます。


4. HパラメータからZパラメータへの変換
Hパラメータの式は下記でした。(再掲)
v₁ = h₁₁ * i₁ + h₁₂ * v₂ 　・・・・・　(3)
i₂ = h₂₁ * i₁ + h₂₂ * v₂ 　・・・・・　(4)

Zパラメータの従属変数はv₁、v₂ですが、(4)式を変形すると
ただちにv₂の式が得られます。
v₂ = -(h₂₁ / h₂₂) * i₁ + 1 / h₂₂ * i₂ 　・・・・・　(4')

Zパラメータの式と比較すると
z₂₁ = -h₂₁ / h₂₂
z₂₂ = 1 / h₂₂

を得ます。次に、v₂を消去するため(4')式を(3)式に代入します。
v₁ = h₁₁ * i₁ + h₁₂ * {-(h₂₁ / h₂₂) * i₁ + 1 / h₂₂ * i₂}
　= h₁₁ * i₁ - (h₁₂ * h₂₁ / h₂₂) * i₁ + (h₁₂ * / h₂₂) * i₂
　= (h₁₁ * h₂₂ - h₁₂ * h₂₁) / h₂₂ * i₁ + (h₁₂ / h₂₂) * i₂

�冑 = h₁₁ * h₂₂ - h₁₂ * h₂₁と 置換えると
v₁ = (�冑 / h₂₂) * i₁ + (h₁₂ / h₂₂) * i₂

Zパラメータの式と比較すると
z₁₁ = �冑 / h₂₂
z₁₂ = h₁₂ / h₂₂

を得ます。


5. YパラメータからHパラメータへの変換
Yパラメータの式は下記でした。(再掲)
i₁ = y₁₁ * v₁ + y₁₂ * v₂ 　・・・・・　(5)
i₂ = y₂₁ * v₁ + y₂₂ * v₂ 　・・・・・　(6)

Hパラメータの従属変数はv₁、i₂ですが、(5)式を変形すると
ただちにv₁の式が得られます。
v₁ = (1 / y₁₁) * i₁ - (y₁₂ / y₁₁) * v₂ 　・・・・・　(5')

Hパラメータの式と比較すると
h₁₁ = 1 / y₁₁
h₁₂ = -y₁₂ / y₁₁

を得ます。次に、v₁を消去するため(5')式を(6)式に代入します。
i₂ = y₂₁ * v₁ + y₂₂ * v₂
　= y₂₁ * {(1 / y₁₁) * i₁ - (y₁₂ / y₁₁) * v₂} + y₂₂ * v₂
　= (y₂₁ / y₁₁) * i₁ - (y₁₂ * y₂₁ / y₁₁) * v₂ + y₂₂ * v₂
　= (y₂₁ / y₁₁) * i₁ + (y₁₁ * y₂₂ - y₁₂ * y₂₁) / y₁₁ * v₂

�凉 = y₁₁ * y₂₂ - y₁₂ * y₂₁と 置換えると
i₂ = (y₂₁ / y₁₁) * i₁ + (�凉 / y₁₁) * v₂

Hパラメータの式と比較すると
h₂₁ = y₂₁ / y₁₁
h₂₂ = �凉 / y₁₁

を得ます。


6. ZパラメータからHパラメータへの変換
Zパラメータの式は下記でした。(再掲)
v₁ = z₁₁ * i₁ + z₁₂ * i₂ 　・・・・・　(1)
v₂ = z₂₁ * i₁ + z₂₂ * i₂ 　・・・・・　(2)

Hパラメータの従属変数はv₁、i₂ですが、(2)式を変形すると
ただちにi₂の式が得られます。
i₂ = -(z₂₁ / z₂₂) * i₁ + (1 / z₂₂) * v₂ 　・・・・・　(2')

Hパラメータの式と比較すると
h₂₁ = -z₂₁ / z₂₂
h₂₂ = 1 / z₂₂

を得ます。次に、i₂を消去するため(2')式を(1)式に代入します。
v₁ = z₁₁ * i₁ + z₁₂ * i₂
　= z₁₁ * i₁ + z₁₂ * {-(z₂₁ / z₂₂) * i₁ + (1 / z₂₂) * v₂}
　= z₁₁ * i₁ + (-z₁₂ * z₂₁ / z₂₂) * i₁ + (z₁₂ / z₂₂) * v₂
　= (z₁₁ * z₂₂ - z₁₂ * z₂₁) / z₂₂ * i₁ + (z₁₂ / z₂₂) * v₂

�凛 = z₁₁ * z₂₂ - z₁₂ * z₂₁と 置換えると
v₁ = (�凛 / z₂₂) * i₁ + (z₁₂ / z₂₂) * v₂

Hパラメータの式と比較すると
h₁₁ = �凛 / z₂₂
h₁₂ = z₁₂ / z₂₂

を得ます。


7. パラメータ変換の一覧表
以上の計算を纏めると下記の表となります。


行列名	Y		Z		H
	y11	y12	z22/�凛	−z12/�凛	1/h11	−h12/h11
	y21	y22	−z21/�凛	z11/�凛	h21/h11	�冑/h11
	y22/�凉	−y12/�凉	z11	z12	�冑/h22	h12/h22
	−y21/�凉	y11/�凉	z21	z22	−h21/h22	1/h22
	1/y11	−y12/y11	�凛/z22	z12/z22	h11	h12
	y21/y11	�凉/y11	−z21/z22	1/z22	h21	h22

(注)�凉 = y₁₁ * y₂₂ - y₁₂ * y₂₁、 �凛 = z₁₁ * z₂₂ - z₁₂ * z₂₁、 �凉 = h₁₁ * h₂₂ - h₁₂ * h₂₁