回路の機能
近い波形になる回路です。
- 微分回路の出力波形例
- 積分回路の出力波形例
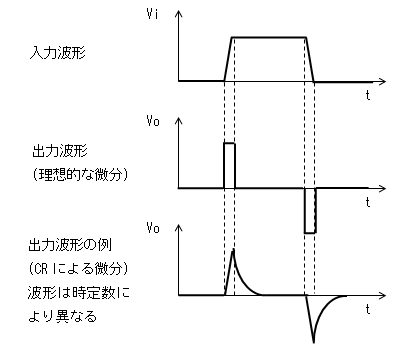
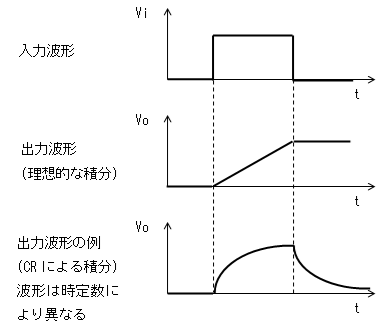
いましたが、前後に接続される回路により動作波形が変わるので、大規模回路の設計に
向いていないことや、コンデンサーを使うのでLSI化に向いていないことなどから、
近年ではあまり使用されません。
回路図
- 微分回路
- 積分回路
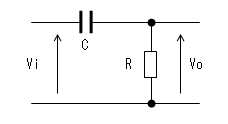
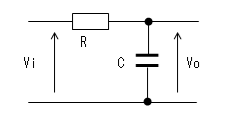
微分回路の動作
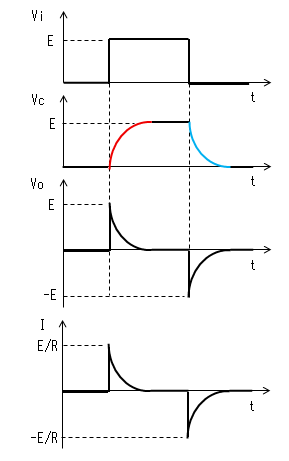
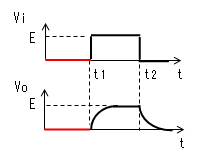
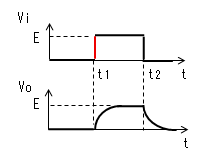
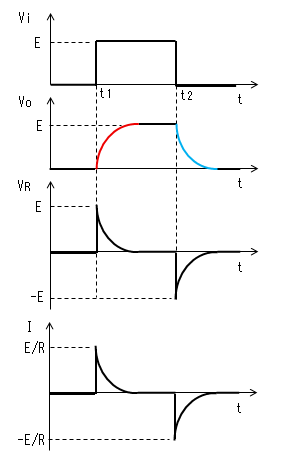
- 「パルス幅≫時定数」のときの動作 初期状態(t=0)でコンデンサー(C)の電荷は0とします。
- 指数関数の曲線 コンデンサーの両端の電圧(Vc)は、電気回路(学)の RC直流回路の過渡応答で
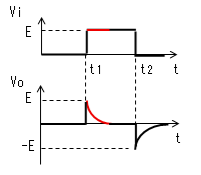
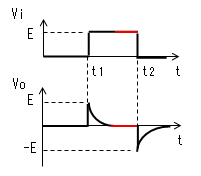
- 「パルス幅≫時定数」が成り立たないときの動作 パルス幅≫時定数が成り立たないときは、時刻t2になったとき
- CR微分回路の問題点 「パルス幅≫時定数」が成り立たないときの動作の項で見たように
入力波形の立上がり、立ち下がり時間は0とします。
また、時定数(C*R)はパルス幅(t2−t1)より十分短いとします。
| 時間(t) | 回路の状態 | 波形 | 動作説明 |
| 0≦t<t1 | 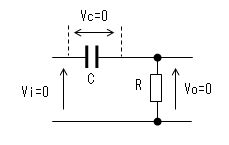 |
 |
コンデンサーの電荷が0なので 両端の電圧(Vc)も0です。 出力(Vo)は抵抗(R)により 直流的にも0[V]です。 |
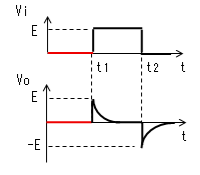
| t=t1 | 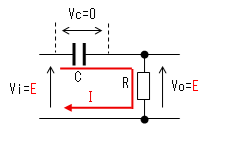 |
 |
時刻t1で入力(Vi)がVi=Eに 立ち上がります。 コンデンサー(C)はすぐに充電 しないので、この瞬間のVcは 0のままです。よって出力電圧 (Vo)もEに立上がります。 コンデンサーから抵抗に電流が 流れ始めますが、この瞬間の 電流IはI=E/Rです。 |
| t1<t≪t2 | 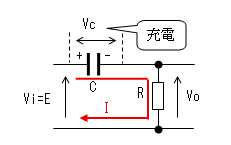 |
 |
電流Iによりコンデンサーが充電 されるのでVcは0から次第に大きく なります。Vcが大きくなるとVoが 次第に小さくなるので、電流Iも 次第に小さくなります。 そのカーブは指数関数です。 |
| t1≪t<t2 | 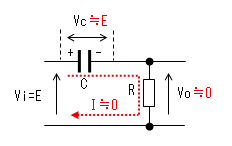 |
 |
時定数がパルス幅より十分 小さいと、時刻がt2になる前に コンデンサーがVc≒Eまで充電 されます。よってVo=E-Vc≒0、 I=Vo/R≒0になります。 |
| t=t2 | 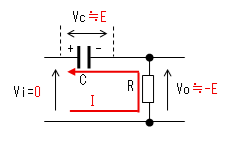 |
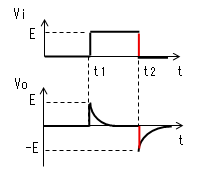 |
時刻t2で入力(Vi)がVi=0に 立ち下がります。 コンデンサー(C)はすぐに放電 しないので、この瞬間のVcは Eのままです。よって出力電圧 (Vo)は−Eに立下がります。 コンデンサーから抵抗に電流が 流れ始めますが、この瞬間の 電流Iは|I|≒E/Rです。 |
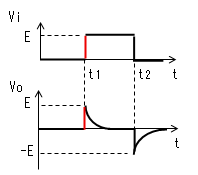
| t2<t | 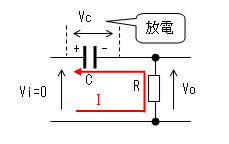 |
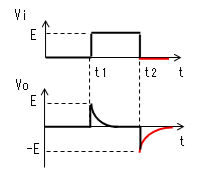 |
電流Iによりコンデンサーが放電 するのでVcはEから次第に小さく なります。Vcが小さくなるとVoは -Eから次第に0に近づくので、 電流Iも次第に小さくなります。 そのカーブは指数関数です。 |
求めた式と曲線になります。(下式のtはViの変化点からの時間)
Vcが立上がるときの波形(下図の赤色部分)は
Vc = E×[1 - exp{-1/(RC)×t}]
Vcが立下がるときの波形(下図の青色部分)は
Vc = E×exp{-1/(RC)×t}
で与えられます。時定数(τ)は
τ= C * R
出力電圧(Vo)は
Vo = E - Vc = E×exp{-1/(RC)×t}
電流Iは
I = Vo / R = E/R×exp{-1/(RC)×t}
となります。
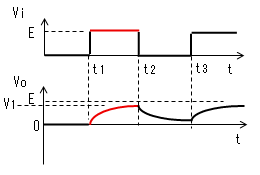
コンデンサの電圧VcはまだEまで充電されていません。
そこで下記のようになります。(t1の直後からの動作)
| 時間(t) | 回路の状態 | 波形 | 動作説明 |
| 0≦t≦t1 | (省略) | (省略) | |
| t1<t<t2 |  |
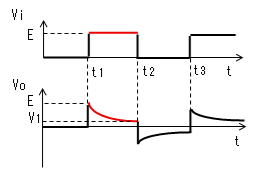 |
電流Iによりコンデンサーが充電 されるのでVcは0から次第に 大きくなりますが、t2になっても Eまで充電しきれず、VoはV1まで しか低下しません。 |
| t=t2 | 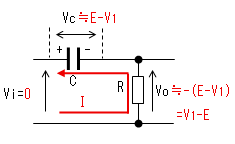 |
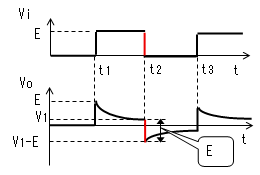 |
時刻t2で入力(Vi)がVi=0に 立ち下がります。 コンデンサー(C)はすぐに放電 しないので、この瞬間のVcは (E-V1)のままです。よって出力電圧 (Vo)は(V1−E)に立下がります。 |
| t2<t<t3 |  |
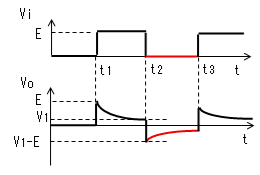 |
電流Iによりコンデンサーが放電 するのでVcは(E-V1)から次第に 小さくなります。Vcが小さくなる とVoは(V1-E)から次第に0に近づき ますが、t3になっても0には なりません。また、定常状態では VoはEに達しません。 |
パルス幅に対し時定数が大きいと出力が微分波形から
かけ離れてしまいます。
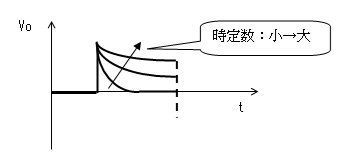
一方、時定数が小さ過ぎると入力波形(Vi)の立上がり時間が有限であるため
下図のように出力波形(Vo)が立上がらなくなってしまいます。
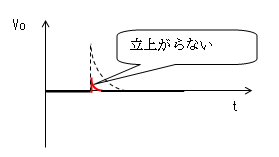
このようにCR微分回路では時定数を適当な値に設定する必要があるのですが、
CR微分回路の次段にインピーダンス:RLの回路が接続される場合、
時定数は{C * (R // RL)}に変化してしまいます。
(// は並列接続の意)
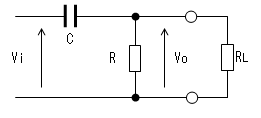
以上のような理由があるため、CR微分回路では入力信号の立上がり時間や
負荷抵抗(RL)をある程度固定していないと、条件が変わる度に
コンデンサーや抵抗の値を調整する必要があることから、とくに大規模な
ディジタル回路などでは使いづらく近年ではあまり使用されなくなりました。
積分回路の動作
- 「パルス幅≫時定数」のときの動作 初期状態(t=0)でコンデンサー(C)の電荷は0とします。
- 指数関数の曲線 コンデンサーの両端の電圧(Vc)は、電気回路(学)の RC直流回路の過渡応答で
- 「パルス幅≫時定数」が成り立たないときの動作 パルス幅≫時定数が成り立たないときは、時刻t2になったとき
入力波形の立上がり、立ち下がり時間は0とします。
また、時定数(C*R)はパルス幅(t2−t1)より十分短いとします。
| 時間(t) | 回路の状態 | 波形 | 動作説明 |
| 0≦t<t1 | 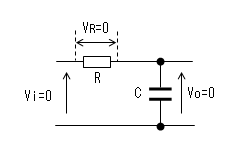 |
 |
コンデンサーの電荷が0なので 両端の電圧も0です。 よって出力(Vo)も0[V]です。 |
| t=t1 | 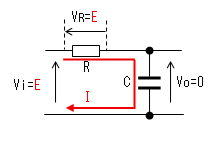 |
 |
時刻t1で入力(Vi)がVi=Eに 立ち上がります。 コンデンサー(C)はすぐに充電 しないので、この瞬間の出力(Vo) は0のままです。抵抗の両端にEの 電圧がかかります。 抵抗からコンデンサーに電流が 流れ始めますが、この瞬間の 電流IはI=E/Rです。 |
| t1<t≪t2 | 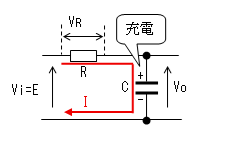 |
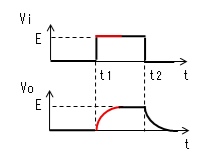 |
電流Iによりコンデンサーが充電 されるのでVoは0から次第に大きく なります。Voが大きくなるとVRが 次第に小さくなるので、電流Iも 次第に小さくなります。 そのカーブは指数関数です。 |
| t1≪t<t2 | 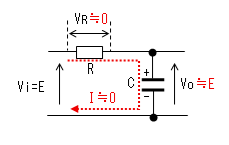 |
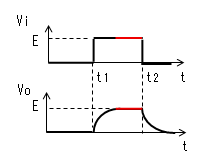 |
時定数がパルス幅より十分小さいと 時刻がt2になる前に、コンデンサー がVo≒Eまで充電されます。 よってVR=E-Vo≒0、I=VR/R≒0に なります。 |
| t=t2 | 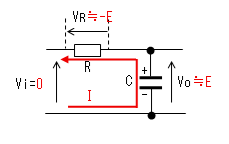 |
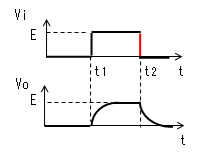 |
時刻t2で入力(Vi)がVi=0に 立ち下がります。 コンデンサー(C)はすぐに放電 しないので、この瞬間のVoは Eのままです。 コンデンサーから抵抗に電流が 流れ始めますが、この瞬間の 電流Iは|I|≒E/Rです。 |
| t2<t | 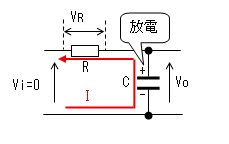 |
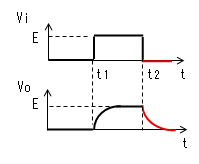 |
電流Iによりコンデンサーが放電 するのでVoはEから次第に小さく なり0に近づくので、電流Iも 次第に小さくなります。 そのカーブは指数関数です。 |
求めた式と曲線になります。(下式のtはViの変化点からの時間)
Voが立上がるときの波形(下図の赤色部分)は
Vo = E×[1 - exp{-1/(RC)×t}]
Voが立下がるときの波形(下図の青色部分)は
Vo = E×exp{-1/(RC)×t}
で与えられます。時定数(τ)は
τ= C * R
抵抗両端の電圧(VR)は
VR = E - Vo = E×exp{-1/(RC)×t}
電流Iは
I = VR / R = E/R×exp{-1/(RC)×t}
となります。
コンデンサの電圧VcはまだEまで充電されていません。
そこで下記のようになります。(t1の直後からの動作)
| 時間(t) | 回路の状態 | 波形 | 動作説明 |
| 0≦t≦t1 | (省略) | (省略) | |
| t1<t<t2 |  |
 |
電流Iによりコンデンサーが充電 されるのでVoは0から次第に大きく なりますが、t2になっても充電 しきれず、VoはV1までしか上昇 しません。 |
| t=t2 | 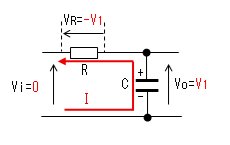 |
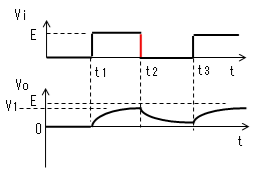 |
時刻t2で入力(Vi)がVi=0に 立ち下がります。 コンデンサー(C)はすぐに放電 しないので、この瞬間のVoは V1のままです。 |
| t2<t<t3 |  |
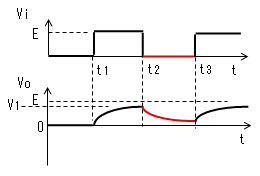 |
電流Iによりコンデンサーが放電 するのでVoはV1から次第に 小さくなり0に近づきますが、 t3になっても0にはなりません。 よって、定常状態では VoはEと0の間を行き来します。 |
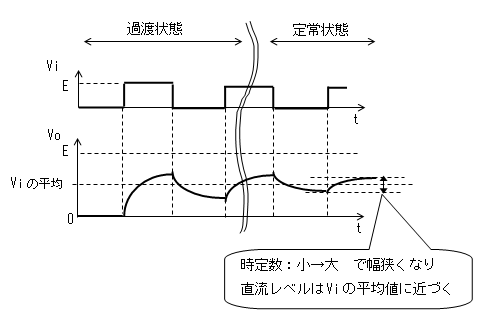
以上のように、時定数を大きくしていくと出力(Vo)の振幅は次第に小さくなり
直流レベルはViの平均値に近づいていきます。
今後の課題
- RL微分回路、LR積分回路の解析 微分・積分回路にはコイルと抵抗を使う方法もありますが、価格や重量・体積などの
- 周波数領域での解析 ここのページでは、CR微分回路・RC積分回路の動作を直流に対する過渡応答
観点からコンデンサーと抵抗を使うことが圧倒的に多かったです。
一方、電源回路などでは、コイルを使うメリットが今でもあるようなので、
別途検討します。
を応用して時間領域から解析しましたが、周波数領域で見た場合
CR微分回路はハイパス・フィルター(ローカット・フィルター)、
RC積分回路はローパス・フィルター(ハイカット・フィルター)
に該当します。
ハイパス・フィルターについては電子回路の CR回路の周波数特性に記載しましたが
ローパス・フィルターについては未完です。(2025/12/13時点)
参考文献
- パルス回路の設計(昭和56年(1981) 第20版(改訂10版)) P-44〜54 微分回路、積分回路、猪飼國夫著、CQ出版社
関連項目
- 電気回路− RC回路の過渡現象
- 電子回路− CR回路の周波数特性