JH8CHUのホームページ>電気回路

電子工作のための　電気回路

工事中(2021/12/20)(2025/12/12)

  1. 電気回路では


  2. 正弦波交流の表し方

    1. 正弦波交流の表し方


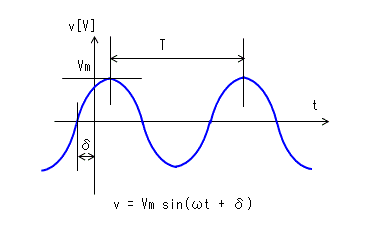
      2. v = Vm * sin(ωt + δ)

      ここに、
      Vm: 最大値
      ω: 角周波数(=2π/T = 2πf)
      δ: 位相
      T : 周期(周期Tの逆数を周波数fといいます。すなわち、f=1/T)

    2. 複素数による表し方

  3. 電気回路素子

      1. 定電圧源

      2. 定電流源

      3. 電気回路素子の電圧と電流
        4. 電気回路素子に交流電圧を印加したとき、素子に流れる電流は下図のようになります。
        ここで交流電圧の瞬時値は
        v=sin(ωt)
        です。
        電気素子回路電圧と電流
        の関係        		電流(瞬時値)消費電力(瞬時値)備考
        抵抗 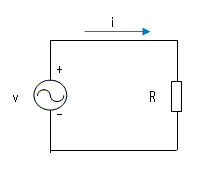v = iR　i=Im sin(ωt)

        　Im=Vm/R        		　p=　
        コンデンサ 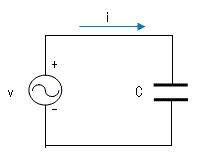v= 1/C ×∫i dt　i=Im sin(ωt+π/2)

        　Im=ωC * Vm        		　p=　
        コイル 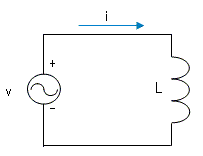v = -L di/dt　i=Im sin(ωt-π/2)

        　Im=Vm/(ωL)        		　p=　

      4. 抵抗
      5. コンデンサの電圧と電流(ボツ)

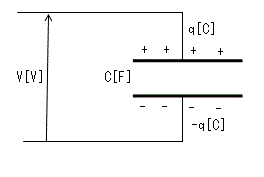
        6. コンデンサに蓄えられる電荷をq、両端の電圧をV
        静電容量をCとすれば、コンデンサにおける基本的な式より
        q = CV
        となります。


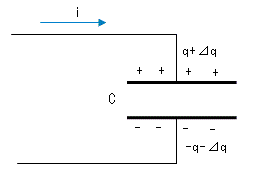
        一方、コンデンサに電流iが流れ込むとき、コンデンサには
        冫[C]の電荷が増加します。
        この現象を数式で表現すると、
        i = dq/dt
        の関係が成り立ちます。


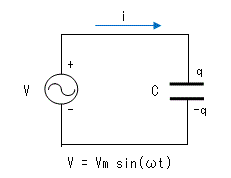
        コンデンサの両端に交流電圧
        V = Vm sim(ωt)
        を印加すると、コンデンサに流れる電流iは
        i = dq/dt = d(CV)/dt = C×dV/dt
        = C×d(Vm sin(ωt)) = C×Vm×d(sin(ωt)
        = C×Vm×ω×cos(ωt)
        = Vm×(Cω)×cos(ωt)
        = Vm×1/(1/Cω)×cos(ωt)
        = Vm/(1/Cω)×sin(ωt+π/2)
        となります。

        この式から、電流iの位相は電圧の位相よりπ/2進むことが
        判ります。また、iの最大値はVm/(1/Cω)ですが、直流における
        オームの法則との対比によりコンデンサの抵抗に相当するのは
        (1/Cω)となります。この抵抗に相当するものは(容量性)リアクタンス
        と呼び、しばしばXcと表現します。

      6. コイルの電圧と電流
      7. 抵抗・コイル・コンデンサの回路
      8. 相互インダクタンスと変圧器
      9. 制御電源
        10. 電気素子回路機能備考
        電圧制御電圧源 　　
        電流制御電圧源 　　
        電流制御電圧源 　　
        電流制御電流源 　　

    1. 直流回路

      1. 電圧と電流(ボツ)
        項目理論的な定義身近な測定器標準器備考
        電圧(電位差)v=∫(a〜b)E・ds 電圧計標準電圧ICなど
        		　
        電流i=dQ/dt 電流計標準電圧IC+標準抵抗器など
        		　

      2. 直流と交流
      3. オームの法則
      4. 直列接続と並列接続
      5. キルヒホッフの法則
      6. 電圧源と電流源
      7. テブナンとノートン

    2. 正弦波交流と複素数表示

      3. これを理解しないと電気回路を学んだことにならない、と言われるくらい
      電気回路の中では重要な概念ですが、その一方で、電磁気学でのベクトル解析や
      半導体理論におけるシュレディンガー方程式やフェルミ準位のように電子工学の
      基礎理論の中では理解の難しいテーマのひとつです。(^_^;

      1. RL直列回路(微分方程式による解法)
      2. RC直列回路(微分方程式による解法)
      3. RLC直列回路(微分方程式による解法)

      4. (複素数による解法)
        5. これまで見てきたように、交流回路を解析するためには微分方程式を解く必要があります。
        しかし、素子がふたつ位であれば、微分方程式を解くことは難しくはありませんが、
        素子の数がもっと増えていくと、もはや微分方程式を解くことは容易ではなくなります。
        そこで、交流電圧や交流電流を複素数で表現する方法が考えられました。
        実数で表現出来るものを、わざわざ複素数で現すのは、かえって面倒になったように
        最初は感じられるものです。

      5. フェーザ表示による解法(ベクトル記号法による解法)
        6. 交流電圧や交流電流を複素数で現すと、実数のまま交流を扱うより回路の解析が
        容易になることを見てきました。
        ところで、線形な回路においては、回路内の電圧や電流の周波数は、回路に接続された
        交流電源の周波数と常に同じになります。
        そうであるならば、交流を表現する際、周波数の項は省略して、位相と大きさのみで
        解析をするようにすると、更に交流回路の扱いが簡単になります。
        このような観点から交流を表現する方法をフェーザ表示と言います。
        そして、フェーザ表示を使用すると交流回路の解析が、直流回路の解析と同様に
        なってしまいまいます。(゜o゜;;

        1. フェーザ表示
          2. 少し、具体的な例を見ていきます。

        2. フェーザ表示による電源の表現
        3. フェーザ表示による交流電圧と交流電流の表現
        4. フェーザ表示による回路の解析

    3. 過渡現象

      1. RC直流回路
          2. (1)充電時
          t=0においてコンデンサーの電荷qは0とします。

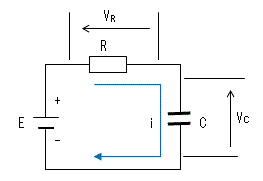
          回路方程式は以下となります。
          E = VC + VR = q/C + Ri　・・・・・(1)

          単位時間に回路を通過した電荷量qは、コンデンサに蓄えられる電荷の
          単位時間あたりの変化量と等しくなるため、次の関係式がなりたちます。
          i = dq/dt　・・・・・(2)

          よって、式(2)を式(1)に代入すると
          E = q/C + R(dq/dt)　・・・・・(3)

          となります。式(3)は変数分離形 の微分方程式であるため、式を変形すると
          1/(q - CE) dq = -1/(RC) dt

          両辺を積分します。
          ∫{1/(q - CE)} dq = -1/(RC) ∫dt

          積分計算をすると
          log(q - CE) = -1/(RC)×t + A

          ここでAは積分定数です。
          ∴q - CE = exp{-1/(RC)×t + A} = exp{-1/(RC)×t}×exp(A)　・・・・・(4)

          ここで初期条件から、t=0のときq=0なので、これらを式(4)に代入すると
          exp(A) = -CE

          このため式(4)は次のようになります。
          q = CE×[1 - exp{-1/(RC)×t}]　・・・・・(5)

          電流iは式(2)よりqの式を時間で微分すればよいので、式(5)を代入して
          i = dq/dt = E/R×exp{-1/(RC)×t}　・・・・・(6)

          式(6)をグラフに表すと


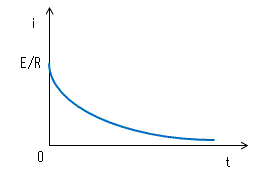
          コンデンサ両端の電圧Vcは
          Vc = q/C

          となることから、この式に式(5)を代入すると、
          Vc = E×[1 - exp{-1/(RC)×t}]　・・・・・(7)

          この式をグラフにすると下図となります。

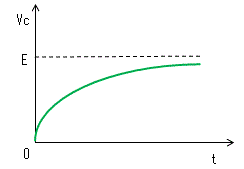
          このように、t=0でVc=0の状態から、抵抗Rを経由してコンデンサが充電されるに従い
          Vc(t)は次第に上昇し、Eに近づいていきます。
          また、(t→∞)のとき、コンデンサに蓄えられる電荷量qはq=CEとなります。

          (2)放電時

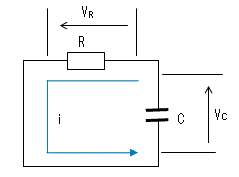
          初期状態においてコンデンサの両端が電圧Eに充電されていて、
          t=0から抵抗Rを経由して電荷が放電される場合を考えます。
          まず、コンデンサに蓄えられている電荷qは
          q = CE　・・・・・(8)

          となります。
          回路方程式は(3)においてE=0とおいたものになります。
          0 = q/C + R(dq/dt)　・・・・・(9)

          変数分離形 の微分方程式ですのでこれを解くと
          q = exp{-1/(RC)×t}×exp(A)　・・・・・(10)

          この式においてt=0のときq=CEとなることから
          CE = exp(A)

          これにより積分定数Aが決まるため、式(10)に代入すると
          q = CE×exp{-1/(RC)×t}　・・・・・(11)

          電流iは式(2)よりqの式を時間で微分すればよいので、式(11)を代入して
          i = dq/dt = -E/R×exp{-1/(RC)×t}　・・・・・(12)

          この式は電流の向きを(1)と同じで計算しているため右辺に−がついていますが
          これは、放電時は充電時と逆に電流が流れるためです。


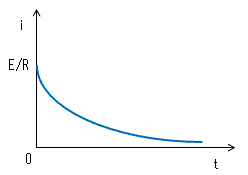
          コンデンサ両端の電圧Vc(t)は、
          Vc = q/Cより
          Vc = E×exp{-1/(RC)×t}　・・・・・(13)

          放電時のVcの波形は下図となります。


          (3)時定数
          過渡現象の変化の早さを表す指標として時定数があります。
          時定数は、過渡現象のグラフの任意の時点における接線が、そのグラフの
          漸近線と交わるまでの時間のことで、しばしばτ(タウ)で表します。
          (定義が解りずらい・・・・笑)
          例えば充電時のVcのグラフのt=0における接線は下図のようになります。
          漸近線はVc=Eですね。


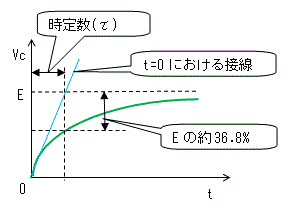
          このVcを例に接線の式を求めます。
          まず(7)式のグラフにおける接線の傾きを求めるために(7)式を微分すると
          Vc/dt = -E×{-1/(RC)}×exp{-1/(RC)×t}
          ∴ Vc/dt = E/(RC)×exp{-1/(RC)×t}　・・・・・(14)

          t=0における接線の傾きは、この式にt=0を代入して
          [Vc/dt]t=0 = E/(RC)×exp(0) = E/(RC)　・・・・・(15)

          となるので接線の式は
          Vc = E/(RC)×t　・・・・・(16)

          この式が漸近線と交わる点では、t=τ、Vc=Eなので(16)式に代入すると
          E = E/(RC)×τ
          ∴ τ = RC　・・・・・(17)

          また、(7)式の時間tがRCになると
          Vc = E×[1 - exp{-1/(RC)×(RC)}] = E×[1 - exp(-1)] ≒ E×0.632

          となることから、Eの値に対して(1-0.632)≒0.368=36.8[%]まで接近します。

          時定数は大きくなるほど、下図のようにグラフの変化が小さく(ゆっくりに)なります。


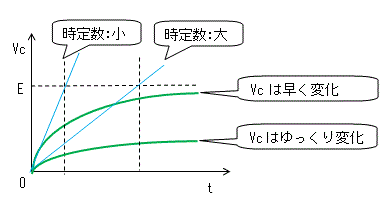
          時定数は慣例的に「じていすう」と読みますが、正しくは「ときていすう」
          と読むと私は学生の時習いました。近年の電気回路学の教科書の
          さくいんを見ると、時定数はしばしば「シ」または「サ行」に
          載ってるようですが、電気学会の「電気回路論(改訂版)」(昭和55年 25版)
          を見ると「ト」の項に分類されています。

      2. R-L直流回路
      3. R-L-C直流回路
      4. RC交流回路
      5. R-L交流回路
      6. R-L-C交流回路

    4. 分布定数回路

    5. MEMO

    JH8CHUのホームページ>電気回路

    Copyright (C)2021, 2025 Masahiro.Matsuda(JH8CHU), all rights reserved.