交流ブリッジによるLC測定(信号源1kHz)

1. 実験の目的

交流ブリッジを使用した電気容量(キャパシタンス)、インダクタンスの
測定原理を理解するとともに、精度が保証されているコンデンサー、
インダクターを交流ブリッジを使用して測定し、どの程度の測定精度が
出るのかを確認します。
今回使用する交流電源は1kHzの正弦波を使用します。


2. 実験課題

1. コンデンサーの容量測定
下記の校正用コンデンサーの静電容量を測定します。


(1)0.1μF 　(誤差1%)
(2)0.01μF　(誤差1%)
(3)1000pF　(誤差1%)
(4)100pF　　(誤差5%)
(5)10pF　　(誤差±0.5pF)



2. インダクタンスの測定
下記の校正用インダクターのインダクタンスを測定します。


(1)10mH　　(誤差5%)
(2)1mH　　　(誤差5%)
(3)100μH　(誤差10%)
(4)10μH　　(誤差10%)
(5)1μH　　(誤差30%)




3. 実験方法

以下、交流ブリッジによる静電容量測定を実験回路(1)と手順(1)に、
インダクタンス測定を実験回路(2)と手順(2)に示します。


1. 実験回路(1)



2. 実験手順(1)

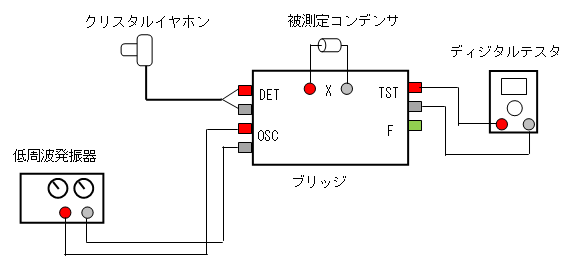
(1)発振器の周波数は1kHzを選択し、出力をレベルを0にします。
(2)ブリッジのトグルスイッチはM側にします。機能設定は「C」(容量測定)を選択します。
(3)実験回路を組立ます。電源は最後にONにします。
(4)被測定コンデンサーを接続します。

(5)発振器の出力レベルを適度な音量まで上げます。
(6)レンジのスイッチとBALANCEのVRとD/FのVRを調整して音が消える点を探します。
(7)音が小さくなったら発振器の出力レベルを上げます。
(8)BALANCEとD/FのVRを調整して音が消える範囲の中央に設定します。
(9)発振器の出力レベルを0にします。(イヤホンから大きな音が出ないようにするため)
(10)ブリッジのトグルスイッチをT側に倒します。
(11)その時の抵抗値をディジタルテスタ(または直流電位差計)で読み取ります。(この値をBとします)
(12)ブリッジのトグルスイッチをM側に倒します。
(13)被測定コンデンサーを交換します。

(14)(5)から(13)までの手順を繰り返します。
　本当は、被測定コンデンサー毎に数回測定し、平均を取るべきですが今回は1回としました。



3. 実験回路(2)



4. 実験手順(2)

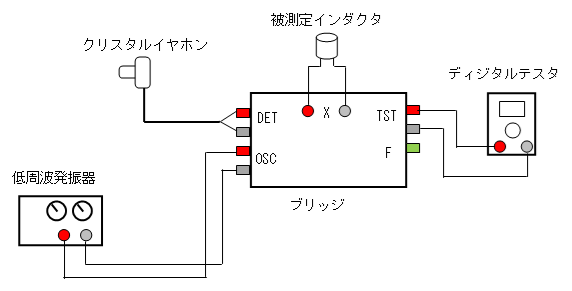
(1)発振器の周波数は1kHzを選択し、出力をレベルを0にします。
(2)ブリッジのトグルスイッチはM側にします。機能設定は「L」(インダクタンス測定)を選択します。
(3)実験回路を組立ます。電源は最後にONにします。
(4)被測定インダクターを接続します。

(5)発振器の出力レベルを適度な音量まで上げます。
(6)レンジのスイッチとBALANCEのVRとQのVRを調整して音が消える点を探します。
(7)音が小さくなったら発振器の出力レベルを上げます。
(8)BALANCEとQのVRを調整して音が消える範囲の中央に設定します。
(9)発振器の出力レベルを0にします。(イヤホンから大きな音が出ないようにするため)
(10)ブリッジのトグルスイッチをT側に倒します。
(11)その時の抵抗値をディジタルテスタ(または直流電位差計)で読み取ります。(この値をBとします)
(12)ブリッジのトグルスイッチをM側に倒します。
(13)被測定インダクターを交換します。

(14)(5)から(13)までの手順を繰り返します。
　本当は、被測定コンデンサー毎に数回測定し、平均を取るべきですが今回は1回としました。



4. 実験機材

1. 交流ブリッジ
2. 低周波発振器
3. クリスタル・イヤホン
4. 校正用コンデンサ
5. 校正用インダクタ
6. ディジタルテスターまたは直流電位差計

5. 実験結果

1. 被測定コンデンサーの容量計算式


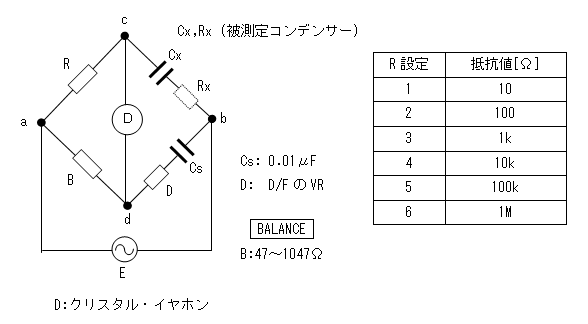
ディジタルテスター(または直流電位差計)の読みをBとします。
Cs = 0.01μF、Rはレンジにより変わります。
このとき、次の式で被測定コンデンサーの容量(Cx)を計算します。

Cx = B/R・Cs


2. 容量の測定結果

Cx公称値[F]	R[レンジ]	R[Ω]	B[Ω]	Cx計算値[F]	公称値からの偏差[%]	50Hzでの測定値(*1)
0.1μ (1%)	1	10	117.0	0.117μ	17.0%	0.1106μ
0.01μ (1%)	2	100	97.1	0.00971μ	-2.9%	0.00967μ
1000p (1%)	3	1k	100.4	1004p	0.4%	1057p
100p (5%)	4	10k	115.9	115.9p	15.9%	測定不可
10p (±0.5p)	5	100k	216.6	21.66	217%	測定不可

(*1)50Hzでの測定結果はこちらの実験結果を引用。


3. 被測定インダクターのインダクタンス計算式


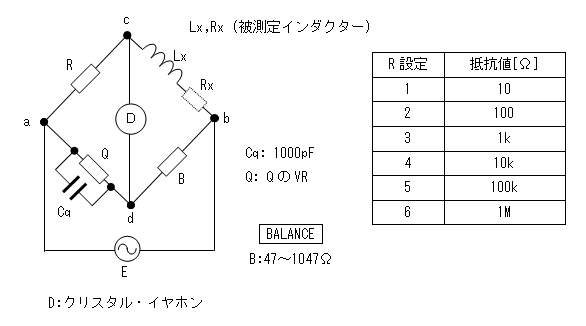
ディジタルテスター(または直流電位差計)の読みをBとします。
Cq = 1000pF、Rはレンジにより変わります。
このとき、次の式で被測定インダクターのインダクタンス(Lx)を計算します。

Lx =R・B・Cq


4. インダクタンスの測定結果

Lx公称値[H]	R[レンジ]	R[Ω]	B[Ω]	Lx計算値[H]	公称値からの偏差[%]	50Hzでの測定値(*1)
10m (5%)	4	10k	822	8.22m	-10.78%	8.51m
1m (5%)	3	1k	777	0.777m	-22.3%	0.838m
100μ (10%)	2	100	868	86.8μ	-13.2%	83.9μ
10μ (10%)	2	100	128.6	12.86μ	28.6%	9.02μ
1μ (30%)	1	10	254.4	2.54μ	254%	0.858μ

(*1)50Hzでの測定結果はこちらの実験結果を引用。



6. 考察

1. 誤差伝搬の法則よると、 Cxの計算式が
Cx = B/R・Cs
であるときのCxの相対誤差は、Rの相対誤差が0.1%、Cqの相対誤差が1%であり、
あとはBのディジタル・テスタ(または直流電位差計)の読み取り誤差ですが、
これを仮に(大き目に)0.5%と仮定すると、合計0.1+1+0.5=1.6%となります。
あとは平衡点(つまりVR-Bの値)をいかに正確に合わせるかで誤差が決まります。


2. 誤差伝搬の法則よると、 Lxの計算式が
Lx =R・B・Cq
であるときのLxの相対誤差は、Rの相対誤差が0.1%、Cqの相対誤差が1%であり、
あとはBのディジタル・テスタ(または直流電位差計)の読み取り誤差ですが、
仮に(大き目に)0.5%と仮定すると、合計0.1+1+0.5=1.6%となります。
あとは平衡点(つまりVR-Bの値)をいかに正確に合わせるかで誤差が決まります。


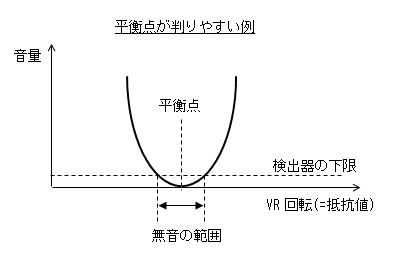
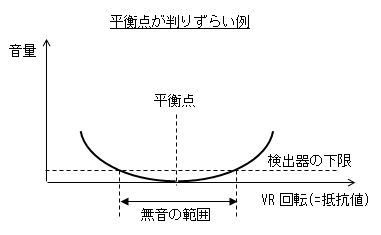
3. 容量測定では、平衡点が比較的判りやすかったですが、
インダクタンス測定では、バランスVR(B)の変化に対して検出器である
イヤホンからの音の変化が小さく、平衡点が判りづらかったです。
この結果、バランスVR(B)を精度よく設定することが難しいことから
測定精度も悪くなります。
この平衡点の位置は、測定の度に多少変化してしまいます。
なので、測定は複数回実施し、平均をとるなどの対策を実施した方が
良いと思います。今回はそこまで実施しませんでした。
　



4. 容量測定の公称値からの偏差は、100pF以上では最大17.0%となりました。
10pFの測定誤差は2倍を超えましたが、実は、X端子にはコンデンサーを接続しなくても
ブリッジが平衡します。ブリッジ自体の浮遊容量と思われ、その値は約11pFでした。
これに、校正用コンデンサーとブリッジ間の配線容量を含めると約15pF大きめの
測定結果が出るようです。なので、1000pF以下の測定では15pFを引くと
10pFあたりまで測定可能と思われます。
50Hzでは測定出来なかった1000pF以下の容量も測定出来たことから、信号源の周波数は
可能な限り高めにすると測定が楽です。(1kHzより3kHzの方がさらに平衡点が見つけやすいです。)


5. インダクタンス測定の公称値からの偏差は、10μH以上では最大28.6%となりました。
1μHの測定誤差は2.5倍にもなりましたが、やはりインダンタンス測定では複数回の
測定が必須と思われます。



7. 参考文献

電気電子工学の基礎実験(1981,第1版第刷)2.4.インピーダンス測定、本岡達著、オーム社


8. 関連項目

1. ソーティ・ブリッジの原理
2. マクスウェル・ブリッジの原理
3. 誤差伝搬の法則
4. 交流ブリッジの製作
5. 低周波発振器
6. 校正用コンデンサ
7. 校正用インダクタ

9. 今後の課題

今のところなし。