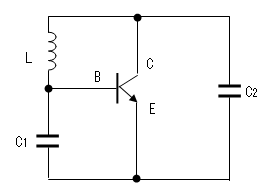
三素子形発振回路
トランジスタの3つの端子間にZ1、Z2、Z3のインピータンスが接続されています。
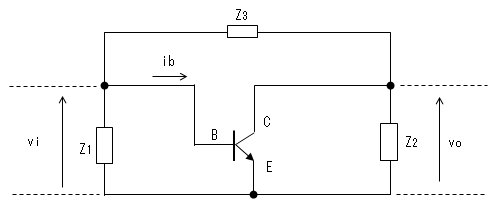
ここで、トランジスタを エミッタ接地の簡略化等価回路で置き換えると、下図となります。
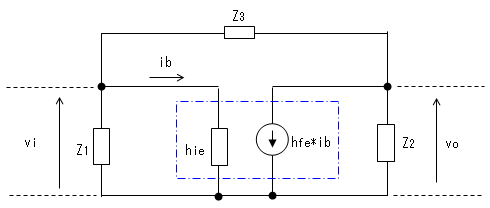
このモデルを使いバルクハウゼンの発振条件を満足するような Z1、Z2、Z3の関係を求めます。
増幅度Gと帰還率Fは電圧で計算してもよいのですが、電流で計算することも出来ます。
三素子形発振回路の解析は電流で計算した方がいくらか計算が楽であると思われます。
電流による解析
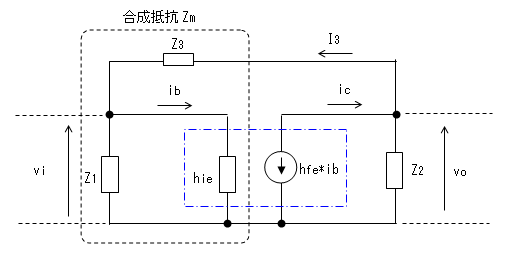
増幅回路の入力電流をib、出力電流をicとすれば、等価回路より 電流増幅度Gは
G = -ic / ib = -hfe * ib / ib
∴ G = -hfe
Z1とhieを並列接続した回路にZ3を直列接続した部分の合成抵抗の値を Zmとすれば、
Zm = Z3 + (Z1 // hie)
∴ Zm = Z3 + (Z1 * hie) / (Z1 + hie)
i3はicをZmとZ2で分流したものなので
i3 = Z2 / (Zm + Z2) * Ic
またibはi3をZ1とhieで分流したものなので
ib = Z1 / (Z1 + hie) * I3
これら2式からi3を消去すると
ib = Z1 / (Z1 + hie) * Z2 / (Zm + Z2) * Ic
帰還率Fは、電流icに対するibの割合なので
F = ib / ic
∴ F = Z1 / (Z1 + hie) * Z2 / (Zm + Z2)
GとFが求まったので、(F * G)を計算すると、
FG = -hfe * Z1 / (Z1 + hie) * Z2 / (Zm + Z2)
Zmを代入して整理します。
FG = -hfe * Z1 / (Z1 + hie) * Z2 / {Z3 + (Z1 * hie) / (Z1 + hie) + Z2}
= -hfe * Z1 / (Z1 + hie) * Z2 / {Z2 + Z3 + (Z1 * hie) / (Z1 + hie)}
= -hfe * Z1 * Z2 / [(Z1 + hie) * {Z2 + Z3 + (Z1 * hie) / (Z1 + hie)}]
= -hfe * Z1 * Z2 / {(Z1 + hie) * (Z2 + Z3) + Z1 * hie}
= -hfe * Z1 * Z2 / {Z1 * (Z2 + Z3) + hie * (Z2 + Z3) + Z1 * hie}
= -hfe * Z1 * Z2 / {Z1 * (Z2 + Z3) + hie * (Z1 + Z2 + Z3)}
ここで、Z1、Z2、Z3が純リアクタンスであるとすれば、
分子の(Z1 * Z2)は実数、分母の第1項のZ1 * (Z2 + Z3)も 実数、分母の第2項の
hie * (Z1 + Z2 + Z3)は虚数となります。
なので、バルクハウゼンの周波数条件であるFVの虚数部が0になるための条件は、
Z1 + Z2 + Z3 = 0 ・・・・・(1)
このとき振幅条件であるFVの実部がFV≧1となるためには
-hfe * Z1 * Z2 / {Z1 * (Z2 + Z3)} ≧ 1
∴ -hfe * Z2 / (Z2 + Z3) ≧ 1
この式に(1)式を代入すると
-hfe * Z2 / (-Z1) ≧ 1
∴ hfe * Z2 / Z1 ≧ 1
∴ hfe ≧ Z1 / Z2 ・・・・・(2)
この式の左辺は正の実数ですので、等号が成り立つためには
右辺も正の実数でなければなりませんから、Z1とZ2の両方が
インダクタンスであるか、またはキャパシタンスである必要があります。
そうすると、(1)式からZ1とZ2がインダクタンスであるならば
Z3はキャパシタンスでなければなりません。
またはZ1とZ2がキャパシタンスであるならばZ3はインダクタンスで
なければなりません。
前者をハートレー回路
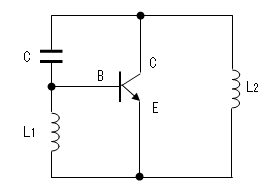
後者をコルピッツ回路
と言います。
電圧による解析
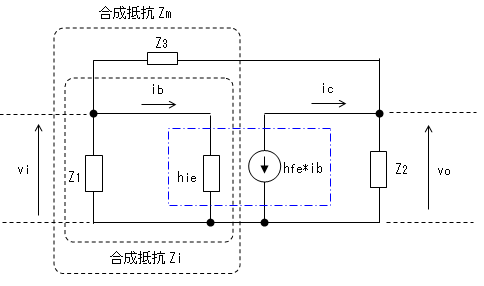
ベースの入力電圧をviとすれば、ベース電流ibは
ib = vi / hie
Z1とhieを並列接続した合成抵抗をZiとすれば
Zi = Z1 // hie = Z1 * hie / (Z1 + hie)
次ににZiとZ3を直列接続した合成抵抗をZmとすれば
Zm = Zi + Z3
さらに、ZmとZ2を並列接続した合成抵抗をZoとすれば
Zo = Zm // Z2
= Zm * Z2 / (Zm + Z2)
この式にZmを代入して消去すると
Zo = (Zi + Z3) * Z2 / (Zi + Z3 + Z2)
トランジスタの出力電圧voはZoに電流源の電流icをかけたものなので
vo = ic * Zo
= -hfe * ib * Zo
ibの式を代入して消去すると
vo = -hfe * vi / hie * Zo
よって電圧増幅度Gは
G = vo / vi = -hfe / hie * Zo
一方、帰還率はvoをZ3とZiと分圧したときの比になるので
F = vi / vo = Zi / (Zi + Z3)
GとFが求まったので、(F * G)を計算すると、
FG = -Zi / (Zi + Z3) * hfe / hie * Zo
Zoの式を代入すると
FG = -Zi / (Zi + Z3) * hfe / hie * (Zi + Z3) * Z2 / (Zi + Z3 + Z2)
(Zi + Z3)は約分できるので
FG = -Zi * hfe / hie * Z2 / (Zi + Z3 + Z2)
この式にZiの式を代入します。だいぶ長くなりました。(-_-;
FG = -{Z1 * hie / (Z1 + hie)} * hfe / hie * Z2 / [{(Z1 * hie / (Z1 + hie)} + Z3 + Z2)]
hieは約分できます。
FG = -{Z1 / (Z1 + hie)} * hfe * Z2 / [{(Z1 * hie / (Z1 + hie)} + Z3 + Z2)]
分母・分子に(Z1 + hie)をかけます。
FG = -Z1 * hfe * Z2 / {Z1 * hie + (Z3 + Z2) * (Z1 + hie)}
分母を整理していきます。
FG = -hfe * Z1 * Z2 / {Z1 * hie + (Z3 + Z2) * Z1 + (Z3 + Z2) * hie}
∴ FG = -hfe * Z1 * Z2 / {(Z3 + Z2) * Z1 + (Z1 + Z2 + Z3) * hie}
ここまでで、電流による解析と同じ式が 求まりました。以下、同じ記述です。
Z1、Z2、Z3が純リアクタンスであるとすれば、
分子の(Z1 * Z2)は実数、分母の第1項のZ1 * (Z2 + Z3)も 実数、分母の第2項の
hie * (Z1 + Z2 + Z3)は虚数となります。
なので、バルクハウゼンの周波数条件であるFVの虚数部が0になるための条件は、
Z1 + Z2 + Z3 = 0 ・・・・・(1)
このとき振幅条件であるFVの実部がFV≧1となるためには
-hfe * Z1 * Z2 / {Z1 * (Z2 + Z3)} ≧ 1
∴ -hfe * Z2 / (Z2 + Z3) ≧ 1
この式に(1)式を代入すると
-hfe * Z2 / (-Z1) ≧ 1
∴ hfe * Z2 / Z1 ≧ 1
∴ hfe ≧ Z1 / Z2 ・・・・・(2)
この式の左辺は正の実数ですので、等号が成り立つためには
右辺も正の実数でなければなりませんから、Z1とZ2の両方が
インダクタンスであるか、またはキャパシタンスである必要があります。
そうすると、(1)式からZ1とZ2がインダクタンスであるならば
Z3はキャパシタンスでなければなりません。
またはZ1とZ2がキャパシタンスであるならばZ3はインダクタンスで
なければなりません。
前者をハートレー回路

後者をコルピッツ回路

と言います。
ハートレー発振回路
結合している場合です。
結合していない場合はM=0で計算します。
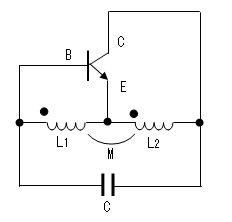
ハートレー発振回路においては発振条件の(1)式の
Z1とZ2はインダクタンス、Z3はキャパシタンスでしたので
Z1 = jω(L1 + M)
Z2 = jω(L2 + M)
Z3 = 1/(jωC)
と置き換えます。そうすると(1)式は
jω(L1 + M) + jω(L2 + M) + 1/(jωC) = 0
となりますので、以下、計算してωの式に変形していくと
jω(L1 + M) + jω(L2 + M) - j/(ωC) = 0
ω(L1 + M) + ω(L2 + M) - 1/(ωC) = 0
ω(L1 + M) + ω(L2 + M) = 1/(ωC)
ω(L1 + L2 +2M) = 1/(ωC)
ω2 = 1/{C * (L1 + L2 +2M)}
∴ ω = 1/√{C * (L1 + L2 +2M)}
ω=2*π*fですので、
f = 1/[2 * π * √{C * (L1 + L2 +2M)}]
M=0の場合は
f = 1/[2 * π * √{C * (L1 + L2)}]
発振条件の(2)式もZ1とZ2を リアクタンスで置き換えると、
hfe ≧ jω(L1 + M) / jω(L2 + M)
∴ hfe ≧ (L1 + M) / (L2 + M)
この式が発振を継続するための振幅条件となります。
さらに、M=0のときは
hfe ≧ L1 / L2
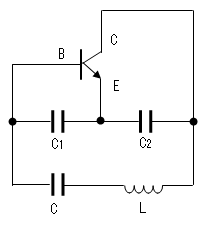
コルピッツ発振回路

コルピッツ発振回路においては発振条件の(1)式の
Z1とZ2はキャパシタンス、Z3はインダクタンスでしたので
Z1 = 1/(jωC1)
Z2 = 1/(jωC2)
Z3 = jωL
と置き換えます。そうすると(1)式は
1/(jωC1) + 1/(jωC2) + jωL = 0
となりますので、以下、計算してωの式に変形していくと
-j/(ωC1) - j/(ωC2) + jωL = 0
-1/(ωC1) - 1/(ωC2) + ωL = 0
ωL = 1/(ωC1) + 1/(ωC2)
ωL = 1/ω * (1/C1 + 1/C2)
ω2 = 1/L * (1/C1 + 1/C2)
∴ ω = √{1/L * (1/C1) + 1/C2)}
ω=2*π*fですので、
f = 1/(2 * π) * √{1/L * (1/C1 + 1/C2)}
∴ f = 1/[2 * π * √{L * C1 * C2 / (C1 + C2)}]
発振条件の(2)式もZ1とZ2を リアクタンスで置き換えると、
hfe ≧ 1/(jωC1) / {1/(jωC2)}
∴ hfe ≧ C2 / C1
この式が発振を継続するための振幅条件となります。
クラップ発振回路(工事中)
これを改善したクラップ発振回路の方が通常よく用いられます。
クラップ発振回路は、コルピッツ発振回路のインダクターLと直列にコンデンサーCを
追加した構成となります。
関連項目
参考文献
- 速解電子回路(1996 初版第7刷) 5.5 発振回路、宮田武雄著、コロナ社
- 電子回路(平成20(2008)年 第1版第1刷) 9章 発振回路、岩田聡編著、オーム社
- 電子回路A(平成8(1996)年 第1版第2刷) 第8章 発振回路の働き、藤原修編著、オーム社
- 入門電子回路(2006 第1版第1刷) 第10章 発振回路、家村道雄監修・家村 他共著、オーム社
- アナログ電子回路の基礎(2003 第1版第1刷) 第11章 発振回路、堀桂太郎著、東京電機大学出版局
- 電子回路の基礎マスター(2009 第1版第1刷) 第4章 発振回路、堀桂太郎監修・船倉一郎著、電気書院