トランジスタのhパラメータ

1. バイポーラ・トランジスタのhパラメータ

Hパラメータの一般的な表現は


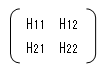
ですが、バイポーラ・トランジスタの場合は慣例的に下記の表現が用いられます。


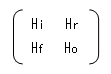
フェーザ表示する必要がないときは、


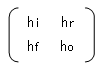
更に、接地方式の違いにより、添え字のi、r、f、oの後の2文字目に
エミッタ接地なら「e」、コレクタ接地なら「c」、ベース接地なら「b」を 追加します。


名称	接続	hパラメータの表現	hパラメータの定義式
エミッタ接地			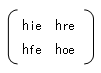vbe = hie×ib + hre×vce　 　ic = hfe×ib + hoe×vce
コレクタ接地			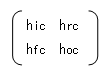vbc = hic×ib + hrc×vec　 　ie = hfc×ib + hoc×vec
ベース接地			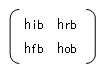veb = hib×ie + hrb×vcb　 　ic = hfb×ie + hob×vcb


各接地方式のhパラメータは、次の関係式を使って相互に変換出来ます。
v_be + v_ec + v_cb = 0　・・・・・　(T1)
i_b + i_e + i_c = 0　・・・・・　(T2)
v_eb = -v_be, v_ce = -v_ec, v_bc = -v_cb　・・・・・　(T3)
v_be << v_cb ≒ v_ce　・・・・・　(T4)




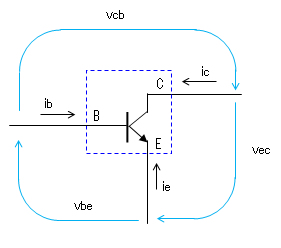
2. バイポーラ・トランジスタのhパラメータの変換

下記の表の式は一部近似式です。


接地方式				備考
エミッタ接地	hie	hic	hib/(1+hfb)
	hre	1-hrc	hib*hob/(1+hfb)-hrb
	hfe	-(1+hfc)	-hfb/(1+hfb)
	hoe	hoc	hob/(1+hfb)
コレクタ接地	hic	hie	hib/(1+hfb)
	hrc	1-hre	1
	hfc	-(1+hfe)	-1/(1+hfb)
	hoc	hoe	hob/(1+hfb)
ベース接地	hib	hie/(1+hfe)	-hic/hfc
	hrb	hie*hoe/(1+hfe)-hre	hrc-hic*hoc/hfc-1
	hfb	-hfe/(1+hfe)	-(1+hfc)/hfc
	hob	hoe/(1+hfe)	-hoc/hfc



1. エミッタ接地からコレクタ接地への変換
エミッタ接地のhパラメータの定義式は下記です。
vbe = hie×ib + hre×vce　・・・・・　(1)
ic = hfe×ib + hoe×vce　・・・・・　(2)

(1)式の右辺に関係式(T1)を代入して、
-vec - vcb = hie×ib + hre×vce
∴　 - vcb　= vec + hie×ib + hre×vce

左辺と右辺第2項に関係式(T3)を代入して、
vbc　= vec + hie×ib - hre×vec
　 = hie×ib + (1 - hre)×vec　・・・・・　(*1)

コレクタ接地のhパラメータの定義式 である
vbc = hic×ib + hrc×vec　
と比較すると
hic = hie
hrc = 1 - hre

(2)式の左辺に関係式(F2)を代入して、
- ib - ie = hfe×ib + hoe×vce
∴　 ie = -ib - hfe×ib - hoe×vce
∴　 ie = -(1 + hfe)×ib - hoe×vce

右辺第2項に関係式(T3) を代入すると
ie = -(1 - hfe)×ib + hoe×vec

コレクタ接地のhパラメータの定義式 である
ie = hfc×ib + hoc×vec　
と比較すると
hfc = -(1 + hfe)
hoc = hoe


2. エミッタ接地からベース接地への変換
エミッタ接地のhパラメータの定義式は下記です。(再掲)
vbe = hie×ib + hre×vce　・・・・・　(1)
ic = hfe×ib + hoe×vce　・・・・・　(2)

これらの式を関係式(T4)の
vce ≒ vcb

を使って近似すると
vbe ≒ hie×ib + hre×vcb　・・・・・　(1')
ic ≒ hfe×ib + hoe×vcb　・・・・・　(2')

(2')式の右辺第1項に関係式(T2)を 代入してibを消去すると、
ic ≒ hfe×(-ie - ic) + hoe×vcb
　 ≒ -hfe×ie - hfe×ic + hoe×vcb
∴　(1 + hfe)×ic ≒ -hfe×ie + hoe×vcb
∴　ic ≒ -hfe/(1 + hfe)×ie + hoe/(1 + hfe)×vcb　・・・・・　(*1)

ベース接地のhパラメータの定義式 である
ic = hfb×ie + hob×vcb　

と比較すると
hfb = -hfe/(1 + hfe)
hob = hoe/(1 + hfe)

(1')式の右辺第1項に関係式(T2)を 代入してibを消去すると、
vbe ≒ hie×(-ie - ic) + hre×vcb
　 ≒ -hie×ie - hie×ic + hre×vcb

この式のicに(*1)式を代入すると
vbe ≒ -hie×ie - hie×{-hfe/(1 + hfe)×ie + hoe/(1 + hfe)×vcb} + hre×vcb
　 ≒ -hie×ie + hie×hfe/(1 + hfe)×ie - hie×hoe/(1 + hfe)×vcb + hre×vcb
　 ≒ hie×{-1 + hfe/(1 + hfe)}×ie - {hie×hoe/(1 + hfe) - hre}×vcb
　 ≒ -hie/(1 + hfe)×ie - {hie×hoe/(1 + hfe) - hre}×vcb

左辺に関係式(T3)を代入して
-veb ≒ -hie/(1 + hfe)×ie - {hie×hoe/(1 + hfe) - hre}×vcb
∴　veb ≒ hie/(1 + hfe)×ie + {hie×hoe/(1 + hfe) - hre}×vcb

ベース接地のhパラメータの定義式 である
veb = hib×ie + hrb×vcb

と比較すると
hib ≒ hie/(1 + hfe)
hrb ≒ hie×hoe/(1 + hfe) - hre


3. コレクタ接地からエミッタ接地への変換
コレクタ接地のhパラメータの定義式は下記です。
vbc = hic×ib + hrc×vec　・・・・・　(3)
ie = hfc×ib + hoc×vec　・・・・・　(4)

(3)式の右辺に関係式(T3)を代入して、
-vcb = hic×ib + hrc×vec

この式の左辺に関係式(T1)を代入して、
-(-vbe - vec) = hic×ib + hrc×vec
∴　vbe + vec = hic×ib + hrc×vec
∴　vbe = hic×ib + hrc×vec - vec
　　　　= hic×ib + (hrc - 1)×vec

右辺第2項に関係式(T3)を代入して、
vbe =　hic×ib + (hrc - 1)×(-vce)
∴　vbe =　hic×ib + (1 - hrc)×vce

エミッタ接地のhパラメータの定義式 である
vbe = hie×ib + hre×vce　

と比較すると
hie = hic
hre = 1 - hrc

(4)式の左辺に関係式(T2)を代入して、
-ib - ic = hfc×ib + hoc×vec
∴　ic = -(1 + hfc)×ib - hoc×vec

右辺第2項に関係式(T3)を代入して、
ic = -(1 + hfc)×ib - hoc×(-vce)
　　= -(1 + hfc)×ib + hoc×vce

エミッタ接地のhパラメータの定義式 である
ic = hfe×ib + hoe×vce　

と比較すると
hfe = -(1 + hfc)
hoe = hoc



4. コレクタ接地からベース接地への変換
コレクタ接地のhパラメータの定義式は下記です。(再掲)
vbc = hic×ib + hrc×vec　・・・・・　(3)
ie = hfc×ib + hoc×vec　・・・・・　(4)

(4)式の右辺第2項に関係式(T3)を代入して、
ie = hfc×ib + hoc×(-vce)

この式を関係式(T4)の
vce ≒ vcb

を使って近似すると
ie ≒ hfc×ib - hoc×vcb　・・・・・　(4')

(4')式の右辺第1項に関係式(T2)を 代入してibを消去すると、
ie ≒ hfc×(-ie - ic) - hoc×vcb
　 ≒ -hfc×ie - hfc×ic - hoc×vcb
∴　hfc×ic ≒ -ie - hfc×ie - hoc×vcb
∴　hfc×ic ≒ -(1 + hfc)×ie - hoc×vcb
∴　ic ≒ -(1 + hfc)/hfc×ie - hoc/hfc×vcb　・・・・・　(*4)
ベース接地のhパラメータの定義式 である
ic = hfb×ie + hob×vcb　

と比較すると
hfb ≒ -(1 + hfc)/hfc
hob ≒ -hoc/hfc

(3)式の左辺に関係式(T3)を代入すると、
-vcb = hic×ib + hrc×vec

左辺に関係式(T1)を代入すると、
-(-vbe - vec) = hic×ib + hrc×vec
∴　vbe + vec = hic×ib + hrc×vec
∴　vbe = hic×ib + hrc×vec - vec
　　　　= hic×ib + (hrc - 1)×vec

この式の左辺と右辺第2項に関係式(T3)を代入すると、
-veb = hic×ib + (hrc - 1)×(-vce)
∴　veb = -hic×ib + (hrc - 1)×vce

この式の右辺第1項に関係式(T2)を 代入してibを消去すると、
veb = -hic×(-ie - ic) + (hrc - 1)×vce
　　= hic×ie + hic×ic + (hrc - 1)×vce

右辺第2項に関係式(T4)を代入して近似すると
vbe ≒ hic×ie + hic×ic + (hrc - 1)×vcb

この式に(*4)式を代入してicを消去すると
veb ≒ hic×ie + hic×{-(1 + hfc)/hfc×ie - hoc/hfc×vcb} + (hrc - 1)×vcb
　　≒ hic×ie - hic×(1 + hfc)/hfc×ie - hic×hoc/hfc×vcb + (hrc - 1)×vcb
　　≒ hic×{1 - (1 + hfc)/hfc}×ie + {-hic×hoc/hfc + (hrc - 1)}×vcb
　　≒ hic×(-1/hfc)×ie + (hrc - hic×hoc/hfc - 1)×vcb
　　≒ -hic/hfc×ie + (hrc - hic×hoc/hfc - 1)×vcb

ベース接地のhパラメータの定義式 である
veb = hib×ie + hrb×vcb　

と比較すると
hib ≒ -hic/hfc
hrb ≒ hrc - hic×hoc/hfc - 1

※hib、hrcは、式の変形過程のどこで近似を実施するかで異なる式になるように思えます。
　最終結果は、参考文献の結論に合わせました。


5. ベース接地からエミッタ接地への変換
ベース接地のhパラメータの定義式は下記です。
veb = hib×ie + hrb×vcb　・・・・・　(5)
ic = hfb×ie + hob×vcb　・・・・・　(6)

これらの式を関係式(T4)の
vce ≒ vcb

を使って近似すると
veb ≒ hib×ie + hrb×vce　・・・・・　(5')
ic ≒ hfb×ie + hob×vce　・・・・・　(6')

(6')式の右辺第1項に関係式(T2)を 代入してieを消去すると
ic ≒ hfb×(-ib - ic) + hob×vce
　　≒ -hfb×ib - hfb×ic + hob×vce
∴　(1 + hfb)×ic ≒ -hfb×ib + hob×vce
∴　ic ≒ -hfb/(1 + hfb)×ib + hob/(1 + hfb)×vce　・・・・・　(*6)

エミッタ接地のhパラメータの定義式 である
ic = hfe×ib + hoe×vce　

と比較すると
hfe ≒ -hfb/(1 + hfb)
hoe ≒ hob/(1 + hfb)

(5')式の右辺第1項に関係式(T2)を 代入してieを消去すると
veb ≒ hib×(-ib - ic) + hrb×vce
　　≒ -hib×ib - hib×ic + hrb×vce

左辺に関係式(T3)を代入して
-vbe ≒ -hib×ib - hib×ic + hrb×vce
∴　vbe ≒ hib×ib + hib×ic - hrb×vce

この式に(*6)式を代入してicを消去すると
vbe ≒ hib×ib + hib×{-hfb/(1 + hfb)×ib + hob/(1 + hfb)×vce} - hrb×vce
　　≒ hib×ib - hib×hfb/(1 + hfb)×ib + hib×hob/(1 + hfb)×vce - hrb×vce
　　≒ hib×{1 - hfb/(1 + hfb)}×ib + {hib×hob/(1 + hfb) - hrb}×vce
　　≒ hib×{1/(1 + hfb)}×ib + {hib×hob/(1 + hfb) - hrb}×vce
　　≒ hib/(1 + hfb)×ib + {hib×hob/(1 + hfb) - hrb}×vce
　
エミッタ接地のhパラメータの定義式 である
vbe = hie×ib + hre×vce　

と比較すると
hie ≒ hib/(1 + hfb)
hre ≒ hib×hob/(1 + hfb) - hrb


6. ベース接地からコレクタ接地への変換
ベース接地の定義式の近似式は下記です。(再掲)
veb ≒ hib×ie + hrb×vce　・・・・・　(5')
ic ≒ hfb×ie + hob×vce　・・・・・　(6')

(6')式の左辺に関係式(T2)を代入して
-ib - ie ≒ hfb×ie + hob×vce
∴　-ie - hfb×ie ≒ ib + hob×vce
∴　-(1 + hfb)×ie ≒ ib + hob×vce
∴　ie ≒ -1/(1 + hfb)×ib - hob/(1 + hfb)×vce

右辺第2項に関係式(T3)を代入して
ie ≒ -1/(1 + hfb)×ib - hob/(1 + hfb)×(-vec)
　≒ -1/(1 + hfb)×ib + hob/(1 + hfb)×vec　・・・・・　(**6)

コレクタ接地のhパラメータの定義式 である
ie = hfc×ib + hoc×vec　

と比較すると
hfc ≒ -1/(1 + hfb)
hoc ≒ hob/(1 + hfb)

ベース接地のhパラメータの定義からの近似式は下記です。(再掲)
veb = hib×ie + hrb×vce　・・・・・　(5')

左辺に関係式(T3)を代入して
-vbe = hib×ie + hrb×vce

さらに左辺に関係式(T1)を代入して
-(-vec - vcb) = hib×ie + hrb×vce
∴　vec + vcb = hib×ie + hrb×vce
∴　vcb = hib×ie - vec + hrb×vce

左辺と右辺第3項に関係式(T3)を代入して
-vbc = hib×ie - vec + hrb×(-vec)
∴　vbc = -hib×ie + vec + hrb×vec

右辺第1項に(**6)式を代入してieを消去すると
vbc ≒ -hib×{-1/(1 + hfb)×ib + hob/(1 + hfb)×vec} + vec + hrb×vec
　　≒ hib/(1 + hfb)×ib - hib×hob/(1 + hfb)×vec + vec + hrb×vec
　　≒ hib/(1 + hfb)×ib + {-hib×hob/(1 + hfb) + hrb + 1}×vec

コレクタ接地のhパラメータの定義式 である
vbc = hic×ib + hrc×vec

と比較すると
hic ≒ hib/(1 + hfb)
hrc ≒ -hib×hob/(1 + hfb) + hrb + 1

となるのですが、文献1によるとhrc ≒ 1です。
どのように近似すると-hib×hob/(1 + hfb) + hrb + 1が1になるのか今のところ
どうしても解りません。(＞o＜???
とりあえず、実務的にはベース接地のhパラメータをコレクタ接地のhパラメータに変換する
必要はほとんどないと思われます。
ので、一旦hrcの計算は保留とします。(-_-;



3. 参考文献

1. 簡明電子回路入門(1980 初版) 第8章 FET、矢部初男著、槇書店