dB(デシベル)
-
増幅度を表すとき、増幅度の値はしばしば大きな値となるので、常用対数を使った
- 電圧利得(Gv) 電圧利得(Gv) = 20 * log|Av| = 20 * log|Vo/Vi|
- 電流利得(Gi) 電圧利得(Gi) = 20 * log|Ai| = 20 * log|Io/Ii|
- 電圧利得(Gp) 電圧利得(Gp) = 10 * log|Ap| = 10 * log|Po/Pi|
dB(デシベル)という単位を使って表します。増幅度をデシベル表示したときの値は
とくに利得と言います。
下図の2端子対回路において、
Pi = Vi * Ii
Po = Vo * Io
です。
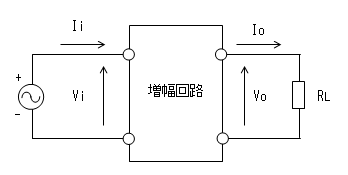
一般的にVi、Ii、Vo、Io、Pi、Poはフェーザ表示となるので、
増幅度Av、Ai、Apもフェーザ表示となります。
(つまり、増幅回路で位相差が発生します。)
利得は下記の式で定義されます。
単位は無名数ですが、いずれもdB(デシベル)という単位を付けます。
慣れないとデシベル表示はピンとこないのですが、電圧なら10倍は20dB、
2倍は6dBとかよく出てくる値を覚えておくと便利です。
3dBもフィルターなどでよく見かけます。
(表の全部を暗記する必要はありません。笑)
| Av,Ai,Ap(倍) | 1 | √2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Gv,Gi[dB] | 0.0 | 3.0 | 6.0 | 9.6 | 12.0 | 14.0 | 15.6 | 17.0 | 18.0 | 19.0 | 20.0 |
| Gp[dB] | 0.0 | 1.5 | 3.0 | 4.8 | 6.0 | 7.0 | 7.8 | 8.5 | 9.0 | 9.5 | 10.0 |
デシベル表示を使ったときの利点は、大きな数を小さな値で表現できることの他に
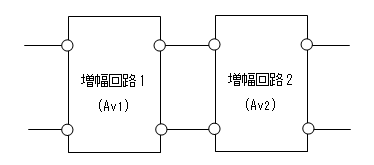
利得計算が簡単になることがあります。例えば、下図のように増幅度がAv1とAv2の
増幅回路を2段接続したとき、全体の増幅度Avは
Av = Av1 * Av2
と掛け算になりますが、利得がそれぞれGv1とGv2であったならば
(つまり、Gv1 = 20 * log|Av1|、Gv2 = 20 * log|Av2|)
全体の利得Gvは
Gv = Gv1 + Gv2
と、足し算になります。
増幅回路の増幅度は必ずしも1以上とは限りません。まれに1未満になることもあります。
また、増幅回路だけではなく、減衰器や伝送路など受動回路にもデシベルの表示を使います。
そうすると、入力よりも出力の方が増幅度(減衰度?)が小さくなるので利得はマイナスになります。
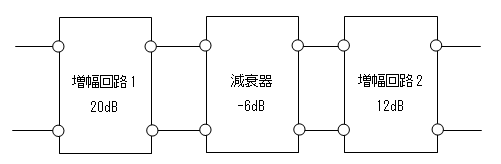
【例】 下図のような回路構成があったとします。
電圧利得20dB(増幅度10倍)の増幅回路1、電圧利得-6dBの減衰器(増幅度?=0.5倍)、
電圧利得12dB(増幅度4倍)の増幅回路2が接続されています。
全体の増幅度(Av)を計算すると
Av = 10 * 0.5 * 4 = 20(倍)
全体の利得(Gv)はいくらになるかと言うと
Gv = 20[dB] - 6[dB] + 12[dB] = 26[dB](20倍)
(26[dB] = 20[dB] + 6[dB]なので、10*2 = 20倍です)
といった感じで使います。こちらの方が簡単ですね。(・・・と、思いますが)
この例ではAvがそれほど大きくないのでご利益を感じませんが(笑)、
80〜100[dB]くらいのレンジになるとウレシサを実感すると思います。
・参考文献
(1)簡明電子回路入門(1980 初版)p-160〜167、矢部初男著、槇書店
(2)電子回路の基礎マスター(2009 第1版第1刷)p-80〜81、船倉一郎著、電気書院
CR回路の周波数特性
-
電子回路では、入力電圧viをコンデンサCと抵抗Rで分圧し、
抵抗の両端の電圧が出力voとなる下図のような回路がよくあらわれます。
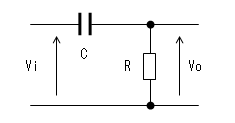
この回路はローカット・フィルタ(Low Cut Filter)を形成します。
すなわち、周波数が低くなると出力電圧voは減衰します。
別名微分回路とも呼ばれます。
最初に定性的な動作を考えます。
コンデンサのインピーダンスは1/(ωC)となるためは周波数が
低いときは1/(ωC)>>Rの関係が成り立ちます。
このため、入力電圧Viはコンデンサと抵抗の分圧回路で
大きく減衰してしまいます。
次に、周波数が高くなり1/(ωC)<<Rの関係が成り立つ周波数帯域では
ほとんど分圧回路で減衰はしなくなるため
Vo ≒ Vi
となり、入力はほとんどそのまま出力に現れます。
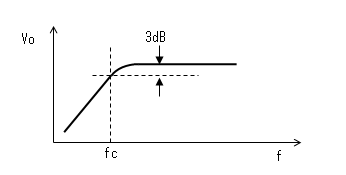
この、出力が減衰し始める境目の周波数をカットオフ周波数と言います。
カットオフ周波数では1/(ωC)=Rです。
また、出力電圧Voは入力電圧Viの 1/√2(=-3dB)となります。
(と言うか、そのようになる周波数をカットオフ周波数と定義した)
カットオフ周波数を求めるために、Voの値を計算します。
ViとVoはともにフェーザ表示です。
Vo = Vi * R / {1/(jωC) + R}
= Vi * R / {R - j/(ωC)}
= Vi * R / [exp(-jθ) * √{R2 + 1/(ωC)2}]
= Vi * exp(jθ) * R / √{R2 + 1/(ωC)2}
ここに、θ= tan-1{(ω * C)/R}
これにより|Vo|が|Vi|の1/√2(=-3dB)になる周波数fcは
1/√2 = R/√{R2 + 1/(ωC)2}
両辺を二乗して
1/2 = R2 /{R2 + 1/(ωC)2}
分母をはらうと
R2 + 1/(ωC)2 = 2 * R2
1/(ωC)2 = R2
両辺の平方根をとって
1/(ωC) = R
∴ω = 1/(C * R)
カットオフ周波数をfcとすれば、ω=2π * fcなので
>fc = 1/(2π * C * R)
となります。
カットオフ周波数より低い周波数領域では-6dB/オクターブの割合で
出力が減衰していきます。
また、カットオフ周波数では、出力は急激に減数し始める訳ではなく、
カットオフ周波数より高い周波数から次第に減衰し始めて
次第に減衰の割合が-6dB/オクターブに近づいていきます。
・参考文献
(1)簡明電子回路入門(1980 初版)p-189〜195、矢部初男著、槇書店
(2)速解電子回路(1996 初版第7刷)p-150〜152、宮田武雄、コロナ社
CR回路の周波数特性(信号源と負荷を考慮した場合)
その場合、下図のように信号源の内部抵抗(Rs)と負荷側の抵抗(RL)が
接続されるため、カットオフ周波数が変化します。
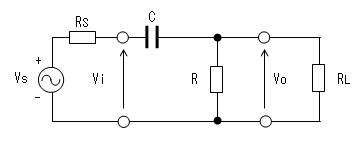
カットオフ周波数を求めるために、Voの値を計算します。
一般的にはVs、Vi、Voはいずれもフェーザ表示です。
まず、RとRLをひとつにまとめてRoと表現します。すなわち
Ro = R // RL = R * RL / (R + RL)
そうすると、
Vo = Vs * Ro / {Rs + 1/(jωC) + Ro}
= Vs * Ro / {Rs - j/(ωC) + Ro}
= Vs * Ro / [exp(-jθ) * √{(Rs + Ro)2 + 1/(ωC)2}]
= Vs * exp(jθ) * Ro / √{(Rs + Ro)2 + 1/(ωC)2}
ここに、θ= tan-1[(ω * C)/(Rs + Ro)]
∴ |Vo| = |Vs| * Ro / √{(Rs + Ro)2 + 1/(ωC)2}
|Vo|の式でω→∞のときの|Vo|を|Voh|とすれば
|Voh| = limω→∞|Vo|
= limω→∞[|Vs| * Ro / √{(Rs + Ro)2 + 1/(ωC)2}]
= |Vs| * Ro / √{(Rs + Ro)2}
= |Vs| * Ro / (Rs + Ro)
|Vo|が|Voh|の1/√2(=-3dB)になる周波数fcは
1/√2 = |Vo| / |Voh|
= [|Vs| * Ro / {√{(Rs + Ro)2 + 1/(ωC)2}] / {|Vs| * Ro / (Rs + Ro)}
= [1 / {√{(Rs + Ro)2 + 1/(ωC)2}] / {1 / (Rs + Ro)}
= (Rs + Ro) / [√{(Rs + Ro)2 + 1/(ωC)2}]
両辺を二乗して
1/2 = (Rs + Ro)2 / {(Rs + Ro)2 + 1/(ωC)2}
分母をはらうと
(Rs + Ro)2 + 1/(ωC)2 = 2 * (Rs + Ro)2
∴ 1/(ωC)2 = (Rs + Ro)2
両辺の平方根をとって
1/(ωC) = Rs + Ro
∴ ω = 1/{C * (Rs + Ro)}
カットオフ周波数をfcとすれば、ω=2π * fcなので
fc = 1/{2π * C * (Rs + Ro)}
となります。
RC回路の周波数特性(工事中)
-
抵抗RとコンデンサCの位置を入れ換えた下図の回路は
ハイカットフィルター(High Cut Filter)を形成します。
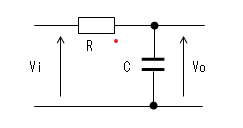
そのカットオフ周波数fcとすれば、
fc = 1/(2π * C * R)
となります。