回路の機能
-
ふたつある入力(vb1、vb2)の差分を増幅した出力が得られる回路です。
出力もふたつ(Vc1、Vc2)ありますが、ふたつの出力は同じ波形で位相が
180°ずれています。出力は必ずしも両方使う必要はありません。
ふたつあるトランジスタのエミッタ端子は共通になっています。
回路図
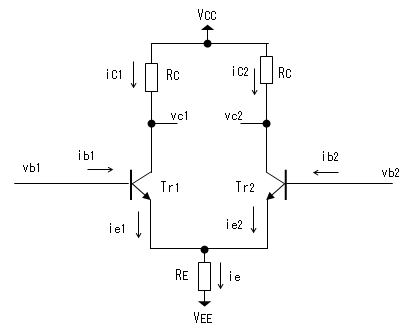
等価回路
また、電源のVCCとVEEは理想的にはインピーダンスが0なので
交流的にはGNDに接続されるのと同じです。結局、等価回路は
下図にようになります。
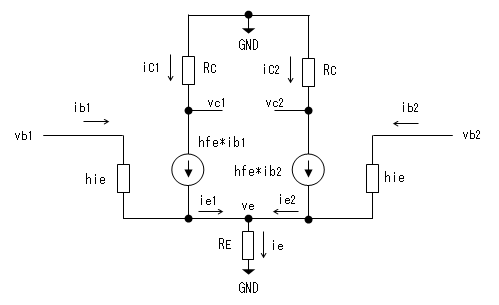
動作の解析と増幅度(1)
-
ふたつあるトランジスタの特性はよくそろっているものとします。
なので、等価回路のhfeとhieはともに等しいと仮定します。
そうすると、等価回路からただちに以下の式が成り立つことが判ります。
vb1 = ib1 * hie + ie * RE ・・・・・ (1)
vb2 = ib2 * hie + ie * RE ・・・・・ (2)
ic1 = hfe * ib1 ・・・・・・・・・・ (3)
ic2 = hfe * ib2 ・・・・・・・・・・ (4)
vc1 = −ic1 * Rc ・・・・・・・・・ (5)
vc2 = −ic2 * Rc ・・・・・・・・・ (6)
ie = ie1 + ie2 = ib1 + ic1 + ib2 + ic2 ・・・・・ (7)
(3)と(4)を(7)に代入して
ie = ib1 + hfe * ib1 + ib2 + hfe * ib2
= (1 + hfe) * ib1 + (1 + hfe) * ib2
= (1 + hfe) * (ib1 + ib2)
≒ hfe * (ib1 + ib2) ・・・・・・ (8)
(∵ hfe >> 1)
一方、(1)と(2)を辺々加えると
vb1 + vb2 = (ib1 + ib2) * hie + 2 * ie * RE ・・・ (9)
(9)に(8)を代入して(ib1 + ib2)を消去すると
vb1 + vb2 ≒ (ie / hfe) * hie + 2 * ie * RE
= ie (hie / hfe + 2 * RE)
= ie (hie + 2 * hfe * RE) / hfe
∴ ie ≒ hfe * (vb1 + vb2) / (hie + 2 * hfe * RE) ・・・ (10)
(10)を(1)に代入して変形していきます。
vb1 ≒ ib1 * hie + {hfe * (vb1 + vb2) / (hie + 2 * hfe * RE)} * RE
右辺の第2項を左辺に移項。
vb1 - {hfe * RE * (vb1 + vb2) / (hie + 2 * hfe * RE)} ≒ ib1 * hie
左辺の分母を通分して
{vb1 * (hie + 2 * hfe * RE) - hfe * RE * (vb1 + vb2)} / (hie + 2 * hfe * RE) ≒ ib1 * hie
左辺の分子のvb1の項をまとめると
{vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (hie + 2 * hfe * RE) ≒ ib1 * hie
両辺をhieで割ると右辺はib1の式になります。
{vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (hie + 2 * hfe * RE) / hie ≒ ib1
これを(3)に代入すると
ic1 ≒ hfe * {vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (hie + 2 * hfe * RE) / hie
さらにこれを(5)に代入すると
vc1 ≒ −hfe * {vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (hie + 2 * hfe * RE) / hie * Rc ・・・ (11)
泣きそうなくらい複雑な式になりました。(>_<)
とりあえず分母では一般的にhie << 2 * hfe * REの関係が成り立つので
近似するとhfeが約分できるので、
vc1 ≒ −hfe * {vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (2 * hfe * RE) / hie * Rc
=−{vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (2 * RE) / hie * Rc
=−Rc * {vb1 * (hie + hfe * RE) - hfe * RE * vb2} / (2 * RE * hie) ・・・ (12)
もう一息です。分子を変形すると
vc1 ≒ −Rc * {hfe * RE * (vb1 - vb2) + hie * vb1 } / (2 * RE * hie) ・・・ (13)
この式の左辺は出力電圧(vc1)、右辺は入力電圧vb1、vb2の式なので
入出力の関係式となります。
いま、vb1とvb2に同じ信号を入力すると vb1 = vb2なので
vc1 ≒ −Rc * {hie * vb1 } / (2 * RE * hie))
= −Rc * vb1 / (2 * RE) ・・・ (14)
このときの利得Acの大きさ|Ac|は
|Ac| = |vc1 / vb1| = Rc / (2 * RE) ・・・ (15)
このAcを同相利得といいます。
次に(13)でvb1とvb2に逆相の信号を入力します。 つまりvb2 = −vb1とすると
vc1 ≒ −Rc * {hfe * RE * (2 * vb1) + hie * vb1 } / (2 * RE * hie)
= −Rc * {(2 * hfe * RE + hie) * vb1} / (2 * RE * hie)
となりますが、ここでhie << 2 * hfe * REの関係を使って近似すると
vc1 ≒ −Rc * {2 * hfe * RE * vb1} / (2 * RE * hie)
= −Rc * (hfe * vb1) / hie ・・・ (16)
このときの利得Adの大きさ|Ad|は
|Ad| = |vc1 / vb1| = Rc * hfe / hie ・・・ (17)
このAdを差動利得といいます。
Acに対するAdの比を同相モード除去比(common mode rejection ratio)
またはCMRRといい、(15)と(17)を使って次の式で与えられます
CMRR = |Ad|/|Ac| = (2 * hfe / hie) * RE ・・・ (18)
ここで(13)の右辺の分母・分子をhieで割って変形すると
vc1 ≒ −Rc * {hfe / hie * RE * (vb1 - vb2) + vb1 } / (2 * RE)
= −Rc * {CMRR / 2 * (vb1 - vb2) + vb1 } / (2 * RE) ・・・ (19)
となります。もしCMRRが十分大きければ、分子の第2項は無視できるので
vc1 ≒ −Rc * {CMRR / 2 * (vb1 - vb2)} / (2 * RE)
= −Rc * {hfe / hie * RE * (vb1 - vb2)} / (2 * RE)
= −Rc * {hfe / hie * (vb1 - vb2)} / 2
∴ vc1 ≒ −{Rc * hfe / (2 * hie)} * (vb1 - vb2) ・・・ (20)
となり、vc1は(vb1 - vb2)に比例することから
この回路を差動増幅回路と言います。
このときの増幅度Avは
Av = vc1 / (vb1 - vb2) = −Rc * hfe / (2 * hie) ・・・ (21)
となりますが、この値は エミッタ接地増幅回路の増幅度の1/2です。
CMRRの値を大きくするためには(18)よりREを大きくすれば良いのですが、
そのためにはREを定電流源に置き換えると性能が向上します。
理想的な定電流源の内部インピーダンスは無限大だからです。
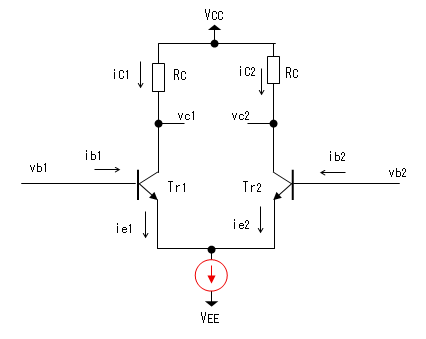
ちなみに、差動出力voを計算すると、
vo = vc1 - vc2 ・・・ (22)
となりますが、(20)と同様に計算すると
(あるいは、vc2はvc1と位相が逆なのでvc2= -vc1)
vc2 ≒ −{Rc * hfe / (2 * hie)} * (vb2 - vb1) ・・・ (23)
となるので、(20)(23)を(22)に代入すると
vo ≒ −(Rc * hfe / hie) * (vb1 - vb2) ・・・ (24)
このときの増幅度Avは
Av = vo / (vb1 - vb2) = −Rc * hfe / hie ・・・ (25)
となり、この値は エミッタ接地増幅回路の増幅度と同じになります。
vc1またはvc2を単独で使うと増幅度がエミッタ接地増幅回路の1/2となり
((21)参照)損した気分になるかもしれませんが、差動出力voとして使うと
同じになるのですね。
出力を直接差動出力として求める
-
前項では出力を対グランド電圧であるvc1として求めたので複雑な式と
なったのですが、これを最初から差動出力(vo = vc1 - vc2)として求めると
計算が無茶苦茶簡単になります。(^^;
まず、
vo = vc1 - vc2 ・・・・・・・・・ (26)
ですが、これに(5)と(6)を代入すると
vo = -ic1 * Rc - (-ic2 * Rc)
= -(ic1 - ic2) * Rc ・・・・・・・・・ (27)
これに(3)と(4)を代入します。
vo = -(hfe * ib1 - hfe * ib2) * Rc
∴ vo = -(ib1 - ib2)* hfe * Rc ・・・・・・・・・ (28)
さらに(1)と(2)を代入してib1とib2を消去すると
vo = -{(vb1 - ie * RE) / hie - (vb2 - ie * RE) / hie} * hfe * Rc
= -{(vb1 - vb2) / hie} * hfe * Rc
= -(vb1 - vb2) * hfe * Rc / hie ・・・・・・・・・ (29)
となり、増幅度は(25)と同じ式になります。
Av = vo / (vb1 - vb2) = −Rc * hfe / hie ・・・ (30)
すなわち、この値は エミッタ接地増幅回路の増幅度と同じです。
動作の解析と増幅度(2)
動作の解析と増幅度(1) では最初にvc1の一般式(13)を求め、この式に条件を代入して
同相利得の式(15)と差動利得の式(17)を導き、そこから更にCMRRが大きいことを条件に
差動増幅の動作を表す(20)式を求めましたが(11)あたりの計算がたいへんでした。(-_-;
ここでは、まず同相利得の式と差動利得の式を導いてから、vc1の増幅度を求めます。
最初はテクニカルな方法に見えるかにもしれませんが、いくらかこちらの方が
計算式が簡単(?)に見えます。
-
まず、出発点となる(1)〜(7)式は同じです。
ふたつあるトランジスタの特性はよくそろっているものとします。
なので、等価回路のhfeとhieはともに等しいと仮定します。
vb1 = ib1 * hie + ie * RE ・・・・・ (1)
vb2 = ib2 * hie + ie * RE ・・・・・ (2)
ic1 = hfe * ib1 ・・・・・・・・・・ (3)
ic2 = hfe * ib2 ・・・・・・・・・・ (4)
vc1 = −ic1 * Rc ・・・・・・・・・ (5)
vc2 = −ic2 * Rc ・・・・・・・・・ (6)
ie = ie1 + ie2 = ib1 + ic1 + ib2 + ic2 ・・・・・ (7)
まず、vb1にたいするvc1の電圧増幅度Av1を計算します。
(1)と(5)を使い
Av1 = vc1 / vb1 = −ic1 * Rc / (ib1 * hie + ie * RE) ・・・・・ (*1)
(3)と(4)を(7)に代入して
ie = ib1 + hfe * ib1 + ib2 + hfe * ib2
= (1 + hfe) * ib1 + (1 + hfe) * ib2
= (1 + hfe) * (ib1 + ib2)
≒ hfe * (ib1 + ib2) ・・・・・・ (8と同じ)
(∵ hfe >> 1)
(*1)に(3)と(8)を代入してieとic1を消去します。
Av1 ≒ −hfe * ib1 * Rc / (ib1 * hie + hfe * (ib1 + ib2) * RE) ・・・・・ (*2)
同相入力の場合vb1=vb2なので、(1)(2)式よりib1=ib2 です。
これを(*2)に代入するとibが消えて同相利得Acが求まります。
Ac ≒ −hfe * ib1 * Rc / (ib1 * hie + hfe * (ib1 + ib1) * RE)
= −hfe * ib1 * Rc / (ib1 * hie + hfe * 2 * ib1 * RE)
∴ Ac ≒ −hfe * Rc / (hie + 2 * hfe * RE) ・・・・・ (*3)
一般的にhie << 2 * hfe * REの関係が成り立つので近似すると
Ac ≒ −hfe * Rc / (2 * hfe * RE)
∴ Ac ≒ −Rc / (2 * RE) ・・・・・ (*4)(15の同相利得の式と同じ)
次に、逆相入力の場合vb2=−vb1なので、(1)(2)を辺々足して
0 = (ib1 + ib2) * hie + 2 * ie * RE ・・・・・ (*5)
これに(8)を代入してieを消去すると
0 = (ib1 + ib2) * hie + 2 * hfe * (ib1 + ib2) * RE
∴ 0 = (ib1 + ib2) * (hie + 2 * hfe * RE) ・・・・・ (*6)
右辺が0になるためにはib2=−ib1です。
これを(*2)に代入するとibが消えて差動利得Adが求まります。
Ad ≒ −hfe * ib1 * Rc / {ib1 * hie + hfe * (ib1 - ib1) * RE}
∴ Ad ≒ −hfe * Rc / hie ・・・・・ (*7)(17の差動利得の式と同じ)
次からがテクニカルな点です。
ふたつの入力電圧vb1とvb2を次のように 同相入力電圧vicomと
差動入力電圧vidiffとに置換え変数変換します。
vicom = (vb1 + vb2) / 2 ・・・・・ (*8)
vidiff = (vb1 - vb2) / 2 ・・・・・ (*9)
逆に(*8)と(*9)をvb1とvb2について解くと
vb1 = vicom + vidiff ・・・・・ (*10)
vb2 = vicom - vidiff ・・・・・ (*11)
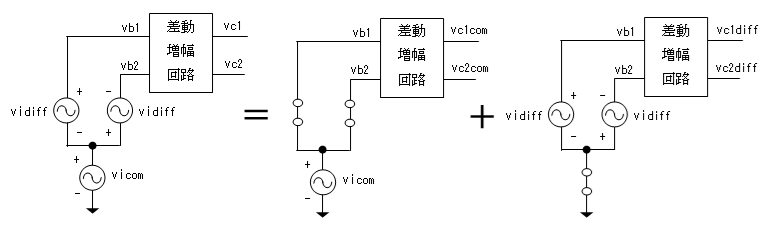
(*10)(*11)よりこれを回路で表すと下図のようになります。
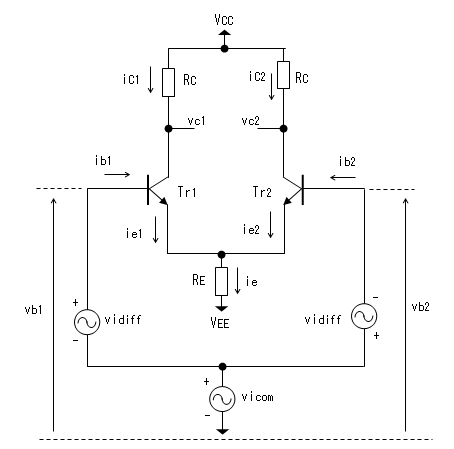
この図を見ると、vicomはvb1とvb2に入力されるので
同相成分であることは明らかです。また、vidiffはvb1とvb2に
逆相成分として入力されることも明らかです。そして、vb1とvb2は
独立に変化しますが、(*10)(*11)からvb1とvb2は vicomとvidiffとで
置換えたものと等価な入力であることが判ります。
ここまで準備しておいて重ね合わせの原理を使います。
差動増幅回路は線形回路なので重ね合わせの原理が成り立ちます。
出力電圧vc1、vc2を求めるにあたり、まず
vicom≠0、かつvidiff=0の出力vc1com、vc2com
を求めます。次に、
vicom=0、かつvidiff≠0の出力vc1diff、vc2diff
を求めます。
一般の状態であるvicom≠0、かつvidiff≠0のときの出力電圧は
重ね合わせの原理により
vc1 = vc1com + vc1diff ・・・・・ (*12)
vc2 = vc2com + vc2diff ・・・・・ (*13)
で求めることが出来ます(下図)。
さて、vicom≠0、かつvidiff=0のとき増幅度をAcとすれば
vc1com = Ac * vicom ・・・・・ (*14)
vc2com = Ac * vicom ・・・・・ (*15)
となります。そしてAcは 本節の(*4)ですでに与えられています。
次に、vicom=0、かつvidiff≠0のときの増幅度をAdとすれば
vc1diff = Ad * vidiff ・・・・・ (*16)
vc2diff = −Ad * vidiff ・・・・・ (*17)
となります。そしてAdは 本節の(*7)ですでに与えられています。
(*12)に(*14)(*16)を代入、(*13)に(*15)(*17)を代入すると
vc1 = Ac * vicom + Ad * vidiff ・・・・・ (*18)
vc2 = Ac * vicom - Ad * vidiff ・・・・・ (*19)
さらに(*18)(*19)に(*4)(*7)(*8)(*9)を代入すると
vc1 = −Rc / (2 * RE) * (vb1 + vb2) / 2 - hfe * Rc / hie * (vb1 - vb2) / 2
vc2 = −Rc / (2 * RE) * (vb1 + vb2) / 2 + hfe * Rc / hie * (vb1 - vb2) / 2
vb1の項とvb2との項でまとめ、整理すると
vc1 = −Rc * {1 / (2 * RE) + hfe / hie} * vb1 / 2 - Rc * {1 / (2 * RE) - hfe / hie} * vb2 / 2 ・・・・・ (*20)
vc2 = −Rc * {1 / (2 * RE) - hfe / hie} * vb1 / 2 - Rc * {1 / (2 * RE) + hfe / hie} * vb2 / 2 ・・・・・ (*21)
{}の中の分母を通分して
vc1 = −Rc * {(hie + 2 * RE * hfe)/ (2 * RE * hie)} * vb1 / 2 - Rc * {(hie - 2 * RE * hfe)/ (2 * RE * hie)} * vb2) / 2 ・・・・・ (*22)
vc2 = −Rc * {(hie - 2 * RE * hfe)/ (2 * RE * hie)} * vb1 / 2 - Rc * {(hie + 2 * RE * hfe)/ (2 * RE * hie)} * vb2) / 2 ・・・・・ (*23)
ここで一般的にhie << (2 * RE * hfe)が成り立つので近似すると
vc1 ≒ −Rc * {(2 * RE * hfe)/ (2 * RE * hie)} * vb1 / 2 - Rc * {(-2 * RE * hfe)/ (2 * RE * hie)} * vb2 / 2
= −Rc * (hfe / hie) * vb1 / 2 - Rc * (-hfe / hie) * vb2) / 2
∴ vc1 ≒ −Rc * (hfe / hie) * (vb1 - vb2) / 2 ・・・・・ (*24)
vc2 ≒ −Rc * {(-2 * RE * hfe)/ (2 * RE * hie)} * vb1 / 2 - Rc * {(2 * RE * hfe)/ (2 * RE * hie)} * vb2) / 2
= −Rc * (-hfe / hie) * vb1 / 2 - Rc * (hfe / hie) * vb2 / 2
∴ vc2 ≒ −Rc * (hfe / hie) * (vb2 - vb1) / 2 ・・・・・ (*25)
これで(20)(23)と同じ式が(*24)(*25)として得られました。
出力インピーダンス
-
制御電流源のインピーダンスは無限大なので、等価回路より
Zo1 = Zo2 = Rc
となります。
差動出力として使う場合は
Zo = 2 * Rc
です。
入力インピーダンス
-
ふたつの入力間のインピーダンスZiは下記となります。
vi = vb1 - vb2
ii = ib1 = −ib2 ・・・ (**1)
なので
Zi = vi / ii = (vi1 - vi2) / ii ・・・ (**2)
この式に(1)、(2)を代入すると
Zi = (ib1 * hie - ib2 * hie) / ii = (ib1 - ib2) * hie / ii ・・・ (**3)
(**1)式を代入すると
Zi = (ii - ( -ii)) * hie / ii = (ii + ii) * hie / ii = 2 * ii * hie / ii
∴ Zi = 2 * hie ・・・ (**4)
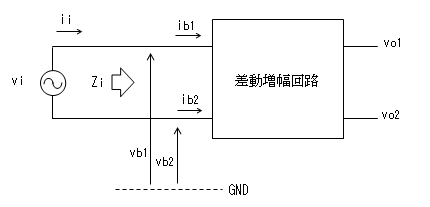
しかし、下図のようにvb1とvb2を別々な信号源vi1と vi2に接続した場合の
入力インピーダンスZi1とZi2が知りたい場合がありそうです。
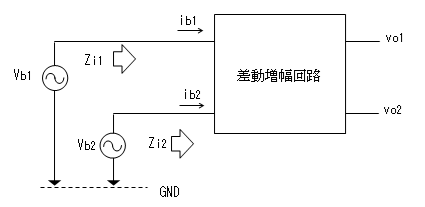
しかし、この場合Zi1はvb2の、Zi2はvb1の 影響を受けて
一定の値にならないと思われます。
参考文献
- 速解電子回路(1996 初版第7刷) 7.2.3 差動増幅回路、宮田武雄著、コロナ社
- 電子回路(平成20(2008)年 第1版第1刷) 6.1 差動増幅回路の特性を知ろう、岩田聡編著、オーム社
- アナログ電子回路の基礎(2003 第1版第1刷) 10.5 差動増幅回路、堀桂太郎著、東京電機大学出版局
- 定本トランジスタ回路の設計(1991 初版) 第11章 差動増幅回路の設計、鈴木雅臣著、CQ出版社
- はじめてのトランジスタ回路設計(1999 初版) P113-118 3石で組むOPアンプ、黒田徹著、CQ出版社
- 実験で学ぶ最新トランジスタ・アンプ設計法(1988 4版) P142-149 差動増幅回路の解析、黒田徹、
ラジオ技術社