ダイオード(PN接合)の静特性グラフ

1. ダイオード(PN接合)の静特性

(1)静特性測定回路


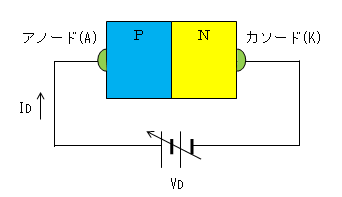
(2)静特性グラフ
ダイオード(PN接合)の電圧(V_D)−電流(I_D)特性を表す
下記の式は半導体や物性の本には必ず出てきます。
この式を初めて見た人の中には腰が引けてしまう方もいるので
ないでしょうか。(少なくとも私はそうでした。)　(^^;

I_D = Is * {exp((q/kT)*V_D) − 1)}

ここに、
Is: 逆方向飽和電流
q: 電子の電荷　(1.60×10^-19 [C])
k: ボルツマン定数　(1.38×10^-23 [J/K])
T: 絶対温度
を示します。

この式の誘導は一旦専門書にまかせるとして、この式をグラフで書くと
下図のようになりますが、なぜこのようなグラフになるか考えてみましょう。




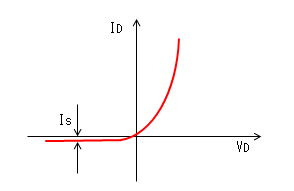
2. ダイオード(PN接合)のグラフ

まず、eを底とする指数関数のグラフは下図となります。
eは無理数で、e=2.71828182845・・・・となる数ですね。
y = e^x


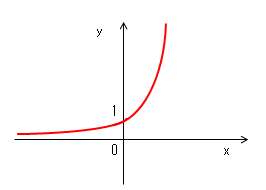
注目点は、
(1)xの変域(-∞〜∞)で常に増加関数である。
(2)グラフがy軸とy=1で交わる。
(3)x→-∞のときy→0。記号で書くとy=lim_x→-∞ = 0。
　　ただし、限りなくx軸に近づきますが、決してx軸には接しません。
　　つまり、x軸は漸近線ですね。
(4)x→∞のときy→∞。記号で書くとy=lim_x→∞ = ∞。

次にxに定数をかけます。
値は(q/kT)です。式としては
y = e^(q/kT)*x

となります。
qは電子の電荷で、値は1.60×10^-19 [C]です。(もちろん電子の電荷は負です)
kはボルツマン定数で、値は1.38×10^-23 [J/K]です。
どちらも高校物理で習います。qは電磁気学の章で、kは熱の章だと思います。
少し悩ましいのはTです。絶対温度なので単位はK(ケルビン)です。
PN接合面の温度なので本来は変数です。が、ここではTを固定して考えてみます。
具体的には室温とされることが多い300K(≒27℃)です。そこで(q/kT)を計算してみると
q/kT = 1.60×10^-19 / (1.38×10^-23 * 300) ≒ 38.6

となります。
なので、y = e^(q/kT)*xのグラフは、y = e^xのグラフを
x方向に約38.6倍した形になります。
が、ここでx軸の目盛りを(1/38.6)倍にしてグラフを書きます。
そうすると、グラフの形は見かけ上y = e^xと同じになります。
y = e^(q/kT)*x


そしてy = e^xのグラフで注目した点(1)〜(4)も全てこのグラフ に当てはまります。

次に、e^(q/kT)*xから1を引きます。
1を引くと、グラフ全体がy軸のマイナス方向に1ずれます。
y = e^(q/kT)*x - 1


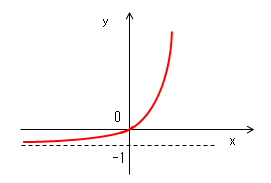
注目点(1)〜(4)がどのように変化するか確認します。
(1)xの変域(-∞〜∞)で常に増加関数である。
(2)グラフが原点でy軸、x軸と交わる。
(3)x→-∞のときy→-1。記号で書くとy=lim_x→-∞ = -1。
　　ただし、限りなくy=-1に近づきますが、決してくy=-1には接しません。
　　つまり、y=-1が漸近線ですね。
(4)x→∞のときy→∞。記号で書くとy=lim_x→∞ = ∞。

最後に{e^(q/kT)*x - 1}に定数Isをかけます。
このIsはダイオードの品種やバラツキで決まる部品固有の値ですが、
実際のIsは温度の関数になると思われます。しかし、ここでも温度は一定と考えると
Isは定数となります。データシート上のIsは多くは1[μA]以下の微少な値です。
そうすると、グラフとしてはy軸方向にIs倍することになります。
が、ここでy軸方向の目盛りを(1/Is)倍するとグラフは見かけ上、
{y = e^(q/kT)*x - 1}のグラフと同じ形になります。
y = Is * {e^(q/kT)*x - 1}


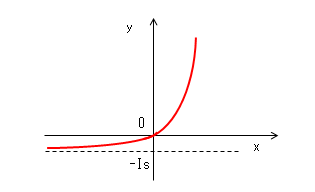
注目点は
(1)xの変域(-∞〜∞)で常に増加関数である。
(2)グラフが原点でy軸、x軸と交わる。
(3)x→-∞のときy→-Is。記号で書くとy=lim_x→-∞ = -Is。
　　ただし、限りなくy=-Isに近づきますが、決してくy=-Isには接しません。
　　つまり、y=-Isが漸近線ですね。
(4)x→∞のときy→∞。記号で書くとy=lim_x→∞ = ∞。

グラフが完成しました。
このグラフで、xをV_Dに、yをI_Dに変更すると、
文献等でよく見かけるダイオードの静特性のグラフになります。
I_D = Is * {exp((q/kT)*V_D) − 1)}


飽和電流Isというのは、実は漸近線のことだったのですね。



3. 既存のダイオードの測定結果を代入してみると

ここで、ダイオードの式に、既存のダイオードの静特性測定結果を代入し、
Isの値を計算してみて、どれくらい一致するか見てみます。
品種としては、(シリコン)ダイオードとして最も名の知れた品種のひとつである1S1588と
シリコン・ショットキーバリア・ダイオードであるBAT43を取り上げてみました。
静特性の測定結果は、ダイオードのデバイス実験結果から、 I_D=6.0[mA]のときの
実測データを拾ってきました。
Is(計算値)はダイオードの静特性の式をIs=の形に変形し、
Is = I_D / {exp((q/kT)*V_D) − 1)}

から計算しました。Tは300Kです。



	1S1588	BAT43	備考
VD	714[mV]	351[mV]
ID	6.0[mA]	6.0[mA]
Is(max,データシート)	0.5[μA]	0.5[μA]
Is(計算値)	6.2-9[μA]	7.7-3[μA]


Ioの値を直接実測することは難しいのですが、1S1588の場合、計算値はあまりに
非現実的に小さいようです。
これに対して、BAT43の計算値はまあまあ1〜2桁くらいの近さがありそうな印象です。
(実際のもれ電流はバラツキや温度の影響が多いと思われます。)

とりあえずの結論ですが、ダイオードの静特性の式である
I_D = Is * {exp((q/kT)*V_D) − 1)}

は、V_Dが0.3[V]くらいのダイオードならば実験値に比較的近いものの、
V_Dが0.6〜0.8[V]くらいの一般的なシリコン・ダイオードでは
実験結果と食い違いが大きくなる、と思われます。

でも、まあ、この式はバイポーラ・トランジスタ回路の解析をする際、とても便利なので
今後もこの式を活用することにします。



4. 参考文献

1. 1S1588データシート
2. BAT43データシート