コレクタ接地(エミッタ・フォロワー)の解析

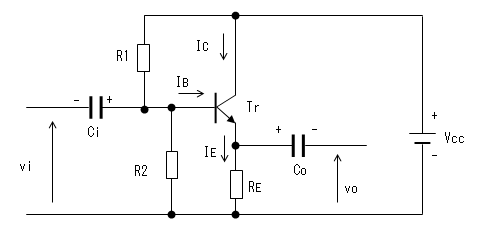
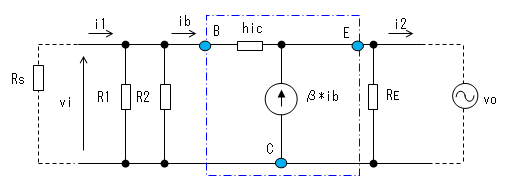
1. 回路図





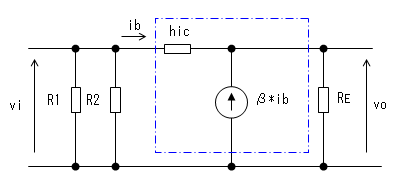
2. 等価回路

増幅回路自体の等価回路は下図にようになります。トランジスタは
コレクタ接地の小信号簡略化等価回路 で置き換えています。コレクタ接地では
入力インピーダンスを考える際は、次段の回路の入力インピーダンス(R_L)が、
出力インピーダンスを考える際は、前段の回路の出力(信号源)インピーダンス(R_S)が
影響するため、計算は少し(かなり?)面倒になります。




3. 入力インピーダンス

1. 解析方法(1)
真面目に(?)計算すると意外とたいへんなので、
以下の手順を考えてみました。


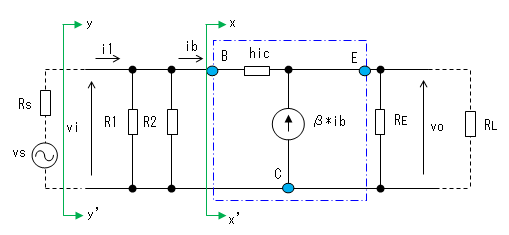
まず最初に、等価回路のx-x'より右側のインピーダンス:Zxを求めます。
キルヒホッフの電圧法則より以下の式が成立します。
(E点から右側に流れ出す電流は、ib + β*ib なので)
vi = hic * ib + (β+1) * ib * R
= [hic + (β+1) * R] * ib

ここに、
R = R_E // R_L

です。// は並列接続の記号です。なので
R_E // R_L = R_E * R_L/(R_E + R_L)

の意味です。また、R_Lは次段の回路の入力インピーダンスです。

Zxはvi/ibであるため、
Zx = vi/ib = hic + (β+1) * R

次にR_B = R1//R2
とすれば、y-y'から右側を見たインピーダンス:Ziは
明らかにR_BとZxを並列に接続したものです。すなわち、
Zi = R_B//Zx
= R_B//{hic + (β+1) * R}

この式と等価回路を比較してみると、Rが(β+1)倍に変換 されている
ところが特徴であり、入力インピーダンスが高くなることが判ります。
なお、ここでhicはhieと同じであり、 hie=1/(40 * IE) × βの概算式を使うことが
できます。また、一般的にβ>>1なので、β+1≒βとしてもよいので、

Zi ≒ R_B//{hie + β * R}



2. 解析方法(2)
真面目に(?)計算する方法により解析します

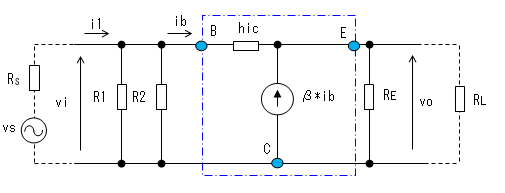
B点、およびE点についてキルヒホッフの電流法則を適用すると、
B点: i1 - Vi/R_B - (Vi - Vo)/hic = 0 ・・・・・・・・・�@
E点: (Vi - Vo)/hic * (β+1) - Vo/R = 0 ・・・・・・・�A

ここに、
R_B = R1//R2
R = R_E//R_L
です。R_Lは次段の回路の入力インピーダンスです。

これらの式の分母を払って整理すると(i1,Vi,Voに着目します)、
hic * R_B * i1 - (hic + R_B) * Vi + R_B * Vo = 0 ・・・・・�B
(β+1) * R * Vi - {(β+1) * R + hic} * Vo = 0 ・・・・・�C

�Cの式を「Vo=」の形に変形します。
Vo = (β+1) * R / {(β+1) * R + hic} * Vi ・・・・・(a)

この式を�Bに代入してVoを消去します。
hic * R_B * i1 - (hic + R_B) * Vi + R_B * (β+1) * R / {(β+1) * R + hic} * Vi = 0

Viの項をまとめます。
hic * R_B * i1 - [(hic + R_B) * {(β+1) * R + hic} - R_B * (β+1) * R] / {(β+1) * R + hic} * Vi = 0

第２項の分子を展開すると、「R_B * (β+1) * R」の項が消えるので、
hic * R_B * i1 - { hic * (β+1) * R + R_B * (β+1) * R + hic²+ R_B * hic - R_B * (β+1) * R} / {(β+1) * R + hic} * Vi = 0
hic * R_B * i1 - { hic * (β+1) * R + hic² + R_B * hic} / {(β+1) * R + hic} * Vi = 0

各項にhicが共通項としてあるので、hicで割ります。
R_B * i1 - {(β+1) * R + hic + R_B} / {(β+1) * R + hic} * Vi = 0

Vi= の形に変形すると、
Vi = R_B * {(β+1) * R + hic} / {(β+1) * R + hic + R_B}* i1

ZiはVi/i1なので、
Zi = Vi/i1
= R_B * {(β+1) * R + hic} / {(β+1) * R + hic + R_B}
= 1/ [{(β+1) * R + hic + R_B}/R_B / {(β+1) * R + hic}]
= 1/ [1/R_B + 1/{(β+1) * R + hic}]

この式は、ZiがR_Bと[(β+1) * R + hic]の並列接続であることを表しています。
すなわち、
Zi = R_B//[(β+1) * R + hic]

ここでhicはhieと同じであり、 hie=1/(40 * IE) × βの概算式を使うことが
できます。また、一般的にβ>>1なので、β+1≒βとしてもよいので、

Zi ≒ R_B//(hie + β*R)

以上が結論ですが、式の変形に疲れました。(^_^;;




4. 出力インピーダンス

1. 解析方法(1)
出力インピーダンスも真面目に(?)計算すると意外とたいへんなので、
まず、簡単な方法で求めます。
出力インピーダンスを求めるためには、等価回路においてvs=0とし
R_Lを取り去って、代わりに信号源(vo)を接続したと考えると下図のようになります。



まず、R1,R2,Rsはそれぞれ並列接続されているので、
R_B = R1//R2
ρ = R_B//Rs
としてR_Bとρを定義します。すると、
E点にキルヒホッフの電流法則を適用すると、
ib + β*ib - vo/R_E - i2 = 0
ib * (β + 1) - vo/R_E - i2 = 0・・・・・・・(b)

ここで、
ib = -vo/(ρ + hic)
の関係があるので、この式を(b)式に代入して変形すると
- vo * (β + 1)/(ρ + hic) - vo/R_E - i2 = 0
- vo * {(β + 1)/(ρ + hic) + 1/R_E} - i2 = 0
vo = - i2 /{(β + 1)/(ρ + hic) + 1/R_E}

従って
Zo = -vo/i2
　= 1 /[(β + 1)/(ρ + hic) + 1/R_E]
　= 1 /[1/{(ρ + hic)/(β + 1)} + 1/R_E]

式の形からZoは{(ρ + hic)/(β + 1)}とR_Eとの並列接続です。従って、
∴ Zo　= {(ρ + hic)/(β + 1)}//R_E

となります。
この式と等価回路を見比べると、(hic + ρ)が1/(β + 1)倍に変換 されて、低くなることが判ります。
ここでもhicはhieと同じであり、 hie=1/(40 * IE) × βの概算式を使うことが
できます。また、一般的にβ>>1なので、β+1≒βとしてもよいので、

∴ Zo　= {(ρ + hie)/β}//R_E


2. 解析方法(2)
真面目に(?)計算する方法により解析します
出力インピーダンスを求めるためには、等価回路においてvs=0とし
R_Lを取り去って、代わりに信号源(vo)を接続したと考えると下図のようになります。

�@、�A式において、i1=-vi/Rs、R_L=∞(∴R=R_E)と置くと
-vi/Rs - Vi/R_B - (Vi - Vo)/hic = 0　・・・・・・・�D
(Vi - Vo)/hic * (β+1) - Vo/R_E - i2= 0　・・・・・�E

ここに、
R_B = R1//R2
です。
これらの式をVi,Vo,i2に着目して整理すると、
- (1/Rs + 1/R_B + 1/hic) * vi + vo/hic = 0　・・・・・・・・�F
(β + 1)/hic * vi - [(β + 1)/hic + 1/R_E] * vo - i2 = 0　・・・�G

�F式を変形して、vi=の形にします。
vi = vo/[hic * (1/Rs + 1/R_B + 1/hic)]
　= vo/[hic * (1/Rs + 1/R_B) + 1]・・・・�H

ここで、ρ=Rs//R_Bと置くと、
1/ρ=1/Rs + 1/R_Bとなるので、�H式は次のようになります。
vi = vo/(hic /ρ + 1)

この式を�G式に代入すると、
(β + 1)/hic * vo/(hic /ρ + 1) - [(β + 1)/hic + 1/R_E] * vo - i2 = 0

第1項の分母分子にρをかけ、voの項を纏めます。また、i2を右辺に移項すると、
[(β + 1)/hic * ρ/(hic + ρ) - (β + 1)/hic - 1/R_E] * vo = i2

vo= の形に変形します。
vo = i2/[(β + 1)/hic * ρ/(hic + ρ) - (β + 1)/hic - 1/R_E]

(β + 1)/hicの共通項があるのでくくり出すと
vo = i2/{(β + 1)/hic * [ρ/(hic + ρ) - 1] - 1/R_E}

[ρ/(hic + ρ) - 1]の中をhic + ρで通分すると分子のρが消えます。
vo = i2/{(β + 1)/hic * [(ρ - hic - ρ)/(hic + ρ)] - 1/R_E}
vo = i2/{(β + 1)/hic * [- hic/(hic + ρ)] - 1/R_E}

分母の第1項の分数は、分母分子にhicがあるので約せます。
vo = i2/{- (β + 1) /(hic + ρ) - 1/R_E}
　= - i2/{(β + 1) /(hic + ρ) + 1/R_E}

Zoはvo/-i2であるので、
Zo = 1/{(β + 1) * /(hic + ρ) + 1/R_E}
　 = 1/{1/[(hic + ρ)/(β + 1)] + 1/R_E}

この式は、Zoが(hic + ρ)/(β + 1)とR_Eの並列接続であることを示しています。
すなわち、
Zo = [(hic + ρ)/(β + 1)]//R_E

この式と等価回路を見比べると、(hic + ρ)が1/(β + 1)倍に変換 されて、
低くなることが判ります。

ここでもhicはhieと同じであり、 hie=1/(40 * IE) × βの概算式を使うことが
できます。また、一般的にβ>>1なので、β+1≒βとしてもよいので、

∴ Zo　= {(ρ + hie)/β}//R_E

と、いう訳でZoの計算も式の変形に疲れました。(^_^;;




5. 電圧増幅度

電圧増幅度:Av = vo/viですが、これは(a)式よりただちに以下のように求まります。
Av = (β+1) * R/{(β+1) * R + hic}

ここに、
R = R_E//R_L
です。また、R_Lは次段の回路の入力インピーダンスです。

ここで、β>>1であることと、 hic ≒ hie ≒ β*γ　(γ=1/[40 * IE]) の近似式を使うと、

Av = R/(R + γ)

更に、R>>γである場合は、

Av ≒ 1

となります。なので、
vo = Av * vi = 1 * vi
∴　vo = vi

となるため、出力電圧は入力電圧に追従することからコレクタ接地は
エミッタ・フォロワとも呼ばれます。




6. 入力コンデンサー(Ci)の影響

入力コンデンサー(Ci)と入力インピーダンス(Zi)はローカット・フィルターを構成します。


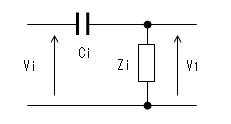
そのカット・オフ周波数(fci)は
fci = 1/(2 * π * Ci * Zi)
∴　fci = 1/{2 * π * Ci * (R_B//(hie + β*R)}

となります。
なお、信号源の内部抵抗(Rs)が無視できない場合、等価回路は下図となります。


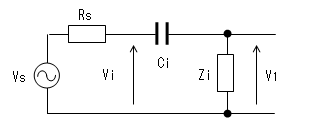
この場合のカットオフ周波数をfciとすれば、ω=2π * fciなので
fci = 1/{2π * Ci * (Rs + Zi)}

となります。
しかし、回路によってはRsの値が特定出来ない場合もあります。
その場合、Rs=0[Ω]がワースト・ケースになるので、
fci = 1/(2π * Ci * Zi)

の式で計算すれば問題ないことになります。



7. 出力コンデンサー(Co)の影響

出力コンデンサー(Co)と出力インピーダンス(Zo)と次段の入力抵抗(Z_L)は
ローカット・フィルターを構成します。


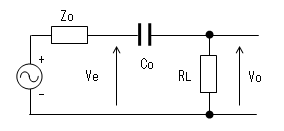
なので、Coの値は、この増幅器の出力側のインピーダンスR_Lが
決まらないと決められません。
そのカットオフ周波数fcoとすれば、
fco = 1/{2 * π * Ci * (Zo + R_L)}
∴　fco = 1/[2 * π * Ci * ({(ρ + hie)/β}//R_E + R_L)]

となります。
R_Lが不定の場合、R_L=0がワースト・ケースになるので、
fco = 1/(2 * π * Ci * Zo)

で計算してもよいでしょう。



8. 参考文献

1. 簡明電子回路入門(1980 初版)、矢部初男著、槇書店
2. 実験で学ぶ最新トランジスタ・アンプ設計法(1988 4版)、黒田徹著、ラジオ技術社