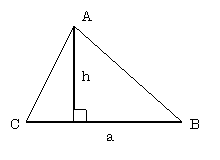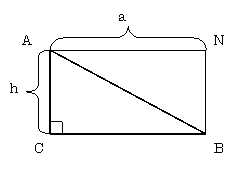三角形の面積

底辺がa、高さがhの三角形の面積をSとすれば
S = ah/2

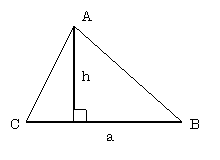
【注意】ここの証明は、幾何学的に厳密ではありません。
常識的に納得出来る(とゆうか筆者の理解出来る範囲での)証明です。(^^;

【証明】
(1)角Cが直角の直角三角形の場合
三角形ABCと合同な三角形ABNを考え、ABを重ね合わせるように配置する。(下図参照)
∠CABと∠CBAの和は∠Rであり、また∠CBA=∠BANであるから、
∠CABと∠BANの和は∠Rであり、すなわち∠CAB=∠Rである。
ゆえに、AC//BN　であり、同様にAN//CB。
従って、四角形ACBNは長方形であるから、その面積S1は、定義より

S1=ab

三角形ABCの面積Sは、四角形の面積S1の1/2であるから、

S = (1/2)S1
=ab/2

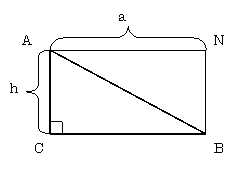
(2)角Cが鋭角の三角形の場合
点Aから辺BCに対して垂線の足を下ろして、その交点をLとすれば、
三角形ALBと三角形ALCはともに直角三角形となる。(下図参照)
ここで、線分BLの長さをxとすれば、線分CL = a - xである。
三角形ALBの面積をS1、三角形ALCの面積をS2とすれば、
(1)よりS1とS2はそれぞれ

S1 = xh/2
S2 = (a - x)h/2

三角形ABCの面積をSとすれば、SはS1とS2の和となるから

S = S1 + S2
= xh/2 + (a - x)h/2
= xh/2 + ah/2 - xh/2
= ah/2

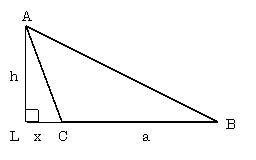
(3)角Cが鈍角の三角形の場合
点Aから線BCに対して垂線の足を下ろして、その交点をLとすれば、
三角形ALBと三角形ALCはともに直角三角形となる。(下図参照)
ここで、線分CLの長さをxとするば、線分BLの長さは(a + b)となる。
三角形ALBの面積をS1、三角形ALCの面積をS2とすれば、
(1)よりよりS1とS2はそれぞれ

S1 = (a + x)h/2
S2 = xh/2

三角形ABCの面積をSとすれば、SはS1からS2を引いたものとなるから

S = S1 - S2
= (a + x)h/2 - xh/2
= ah/2 + xh/2 - xh/2
= ah/2

角Cがいずれの場合も、三角形の面積Sは、底辺a×高さh/2となる。すなわち、

S = ab/2

【証明終】
2006/07/29

JH8CHUのホームページ>数学公式集>三角形の面積